题目内容
11.如果一个正整数能表示成两个连续偶数的平方差,那么称这个正整数为“神秘数”.如4=22-02,12=42-22,20=62-42,则说明4,12,20都是神秘数.(1)28和2012是神秘数吗?为什么?
(2)设两个连续偶数为2k和2k+2(k为非负整数),由这两个连续偶数构成的神秘数是4的倍数吗?
(3)两个连续奇数(取正整数)的平方差是神秘数吗?为什么?
分析 (1)根据“神秘数”的定义,只需看能否把28和2012这两个数写成两个连续偶数的平方差即可判断;
(2)运用平方差公式进行计算,进而判断即可;
(3)运用平方差公式进行计算,进而判断即可.
解答 解:(1)∵28=82-62,2012=5042-5022,
∴28是“神秘数”;2012是“神秘数”;
(2)两个连续偶数构成的“神秘数”是4的倍数.理由如下:
(2k+2)2-(2k)2=(2k+2+2k)(2k+2-2k)=2(4k+2)=4(2k+1),
∴两个连续偶数构成的“神秘数”是4的倍数,
∵2k+1是奇数,
∴它是4的倍数,不是8的倍数;
(3)设两个连续的奇数为:2k+1,2k-1,则
(2k+1)2-(2k-1)2=8k,
此数是8的倍数,而由(2)知“神秘数”是4的倍数,但不是8的倍数,
所以两个连续的奇数的平方差不是神秘数.
点评 此题主要考查了平方差公式的应用,此题是一道新定义题目,熟练记忆平方差公式是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.使一次函数y=(m+2)x+m-2不经过第二象限,且使关于x的不等式组$\left\{\begin{array}{l}{x>m-2}\\{-3x+2≥6m-1}\end{array}\right.$有解的所有整数m的和为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
3.如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):

(1)填写下表:
(2)前5个正方形分割的三角形的和40前n个正方形分割的三角形的和n2+3n,
(3)原正方形能否被分割成2 012个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.

(1)填写下表:
| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
| 分割成的三角形的个数 | 4 | 6 | … |
(3)原正方形能否被分割成2 012个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
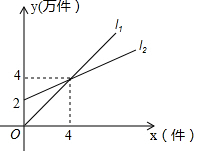 如图,l1表示某产品一天的销售收入与销售量的关系;l2表示该产品一天的销售成本与销售量的关系.则销售收入y1与销售量之间的函数关系式y1=x,销售成本y2与销售量之间的函数关系式y2=$\frac{1}{2}$x+2,当一天的销售量超过x>4时,生产该产品才能获利.(提示:利润=收入-成本)
如图,l1表示某产品一天的销售收入与销售量的关系;l2表示该产品一天的销售成本与销售量的关系.则销售收入y1与销售量之间的函数关系式y1=x,销售成本y2与销售量之间的函数关系式y2=$\frac{1}{2}$x+2,当一天的销售量超过x>4时,生产该产品才能获利.(提示:利润=收入-成本)