题目内容
2.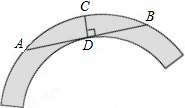 如图是一个圆环形黄花梨木摆件的残片,为求其外圆半径,小林在外圆上任取一点A,然后过点A作AB与残片的内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=15cm,AB=60cm,则这个摆件的外圆半径是37.5cm.
如图是一个圆环形黄花梨木摆件的残片,为求其外圆半径,小林在外圆上任取一点A,然后过点A作AB与残片的内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=15cm,AB=60cm,则这个摆件的外圆半径是37.5cm.
分析 根据垂径定理求得AD=30cm,然后根据勾股定理得出方程,解方程即可求得半径.
解答 解:如图,设点O为外圆的圆心,连接OA和OC,
∵CD=15cm,AB=60cm,
∵CD⊥AB,
∴OC⊥AB,
∴AD=$\frac{1}{2}$AB=30cm,
∴设半径为rcm,则OD=(r-15)cm,
根据题意得:r2=(r-15)2+302,
解得:r=37.5.
∴这个摆件的外圆半径长为37.5cm;
故答案为:37.5.
点评 本题考查了垂径定理的应用以及勾股定理的应用,作出辅助线构建直角三角形是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14. 有理数a,b在数轴上的位置如图所示,则下列各式成立的是( )
有理数a,b在数轴上的位置如图所示,则下列各式成立的是( )
 有理数a,b在数轴上的位置如图所示,则下列各式成立的是( )
有理数a,b在数轴上的位置如图所示,则下列各式成立的是( )| A. | a>-b | B. | -b>0 | C. | b-a>0 | D. | -ab<0 |
 我国南宋数学家杨辉所著的《详解九章算术》一书中用如图解释了二项和的乘方规律,这个图给出了(a+b)n(其中n=1,2,3,4,…)的展开式的系数规律,请根据这个规律写出(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5.
我国南宋数学家杨辉所著的《详解九章算术》一书中用如图解释了二项和的乘方规律,这个图给出了(a+b)n(其中n=1,2,3,4,…)的展开式的系数规律,请根据这个规律写出(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5.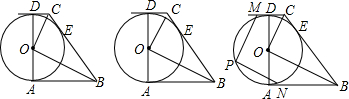
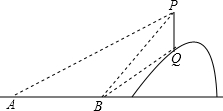 如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是26.6°,向前走30米到达B点,测得杆顶端点P和杆底端点Q的仰角分别是45°和33.7°,求该电线杆PQ的高度(结果精确到1米)
如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是26.6°,向前走30米到达B点,测得杆顶端点P和杆底端点Q的仰角分别是45°和33.7°,求该电线杆PQ的高度(结果精确到1米)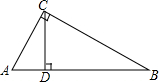 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=3,BD=6,求∠ACD的各个三角函数值.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=3,BD=6,求∠ACD的各个三角函数值.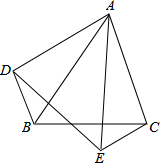 如图,△ABC和△AED中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD、CE,求证:BD=EC.
如图,△ABC和△AED中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD、CE,求证:BD=EC.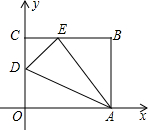 如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,
如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,