题目内容
16.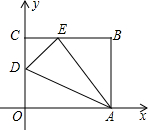 如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,
如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,(1)求D、E两点的坐标.
(2)求过D、E两点的直线函数表达式.
分析 (1)根据折叠的性质,可得AE=AO,OD=ED,根据勾股定理,可得EB的长,根据线段的和差,可得CE的长,可得E点坐标;再根据勾股定理,可得OD的长,可得D点坐标;
(2)根据待定系数法,可得函数解析式.
解答 解:(1)依题意可知,折痕AD是四边形OAED的对称轴, 在Rt△ABE中,AE=AO=10,AB=OC=8,
在Rt△ABE中,AE=AO=10,AB=OC=8,
由勾股定理,得BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=6,
CE=BC-BE=10-6=4,E(4,8).
在Rt△DCE中,由勾股定理,得DC2+CE2=DE2,
又DE=OD,CD=8-OD,
(8-OD)2+42=OD2,
解得OD=5,D(0,5).
所以D(0,5),E(4,8);
(2)设D、E两点所在的直线的解析式为y=kx+b,
则$\left\{\begin{array}{l}{4k+b=8}\\{b=5}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=5}\end{array}\right.$,
所以过D、E两点的直线函数表达式为y=$\frac{3}{4}$x+5.
点评 本题主要考查了翻折变换、勾股定理以及待定系数法求一次函数解析式等知识点,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.

练习册系列答案
相关题目
1.已知(m-n)2=32,(m+n)2=4000,则m2+n2的值为( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 4032 |
5.如果2x与x-3的值互为相反数,那么x等于( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
6.若二项式16m4+4m2加上一个单项式后构成的三项式是一个完全平方式,则这样的单项式的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
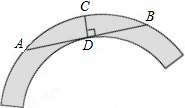 如图是一个圆环形黄花梨木摆件的残片,为求其外圆半径,小林在外圆上任取一点A,然后过点A作AB与残片的内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=15cm,AB=60cm,则这个摆件的外圆半径是37.5cm.
如图是一个圆环形黄花梨木摆件的残片,为求其外圆半径,小林在外圆上任取一点A,然后过点A作AB与残片的内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=15cm,AB=60cm,则这个摆件的外圆半径是37.5cm. 如图,等边△ABC的边长为12cm,D为AC边上一动点,E为AB延长线上一动点,DE交CB于P,点P为DE中点.
如图,等边△ABC的边长为12cm,D为AC边上一动点,E为AB延长线上一动点,DE交CB于P,点P为DE中点.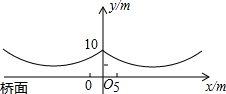 如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,左边的一条抛物线可以用y=$\frac{9}{400}$x2+$\frac{9}{10}$x+10表示,而且左、右两条抛物线关于y轴对称.
如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,左边的一条抛物线可以用y=$\frac{9}{400}$x2+$\frac{9}{10}$x+10表示,而且左、右两条抛物线关于y轴对称.