题目内容
15.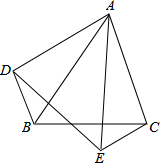 如图,△ABC和△AED中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD、CE,求证:BD=EC.
如图,△ABC和△AED中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD、CE,求证:BD=EC.
分析 根据角与角之间的等量关系求出∠BAD=∠EAC,根据SAS证△BAD≌△EAC,根据全等三角形的性质即可得出结论.
解答 证明:∵∠DAE=∠BAC,
∴∠DAE-∠BAE=∠EAC-∠BAE,
∴∠BAD=∠EAC,
在△BAD和△EAC中,$\left\{\begin{array}{l}{AB=AE}&{\;}\\{∠BAD=∠EAC}&{\;}\\{AD=AC}&{\;}\end{array}\right.$
∴△BAD≌△EAC(SAS),
∴BD=EC.
点评 本题考查了全等三角形的判定与性质;证明三角形全等得出对应边相等是解决问题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
5.如果2x与x-3的值互为相反数,那么x等于( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
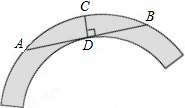 如图是一个圆环形黄花梨木摆件的残片,为求其外圆半径,小林在外圆上任取一点A,然后过点A作AB与残片的内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=15cm,AB=60cm,则这个摆件的外圆半径是37.5cm.
如图是一个圆环形黄花梨木摆件的残片,为求其外圆半径,小林在外圆上任取一点A,然后过点A作AB与残片的内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=15cm,AB=60cm,则这个摆件的外圆半径是37.5cm.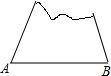 一个缺角的三角形残片如图所示,不恢复这个残角,你能否作出AB边上的高所在的直线?试说明理由.
一个缺角的三角形残片如图所示,不恢复这个残角,你能否作出AB边上的高所在的直线?试说明理由. 如图,在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=$\frac{1}{2}$BD,DF⊥AB于F.求证:CD=DF.
如图,在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=$\frac{1}{2}$BD,DF⊥AB于F.求证:CD=DF.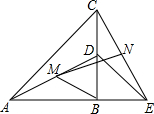 如图,点B为AE上一点,点D在BC上,AB=BC,BD=BE,∠ABC=90°,M、N分别是AD、CE的中点,求∠BMN的度数.
如图,点B为AE上一点,点D在BC上,AB=BC,BD=BE,∠ABC=90°,M、N分别是AD、CE的中点,求∠BMN的度数. 如图,等边△ABC的边长为12cm,D为AC边上一动点,E为AB延长线上一动点,DE交CB于P,点P为DE中点.
如图,等边△ABC的边长为12cm,D为AC边上一动点,E为AB延长线上一动点,DE交CB于P,点P为DE中点.