题目内容
12.如果关于x、y的单项式2axcy与单项式3bx3y是同类项,并且2axcy+3bx3y=0(xy≠0),当m的倒数是-1,n的相反数是$\frac{1}{2}$时,求(2a+3b)99+mc-nc的值.分析 首先利用倒数、相反数的定义得出m,n的值,再利用同类项的定义得出c的值,进而代入求出答案.
解答 解:∵m的倒数是-1,n的相反数是$\frac{1}{2}$,
∴m=-1,n=$-\frac{1}{2}$,
∵关于x、y的单项式2axcy与单项式3bx3y是同类项,
∴c=3,
∵2axcy+3bx3y=0,
∴2a+3b=0,
∴(2a+3b)99+mc-nc
=099+(-1)3-$(-\frac{1}{2}{)^3}$
=$-\frac{7}{8}$.
点评 此题主要考查了倒数、相反数、同类项的定义,正确把握相关定义得出m,n的值是解题关键.

练习册系列答案
相关题目
3.在四个数$\sqrt{3}$,$\sqrt{2}$,1.7,2中,最大的是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1.7 | D. | 2 |
 如图,直线AB,CD交于点O,OE⊥AB,∠DOF=90°,OB平分∠DOG,给出下列结论:①当∠AOF=60°时,∠DOE=60°;②OD为∠EOG的角平分线;③与∠BOD相等的角有三个;④∠COG=∠AOB-2∠EOF,其中正确的结论有①③④(把所有正确结论的序号都填在横线上)
如图,直线AB,CD交于点O,OE⊥AB,∠DOF=90°,OB平分∠DOG,给出下列结论:①当∠AOF=60°时,∠DOE=60°;②OD为∠EOG的角平分线;③与∠BOD相等的角有三个;④∠COG=∠AOB-2∠EOF,其中正确的结论有①③④(把所有正确结论的序号都填在横线上)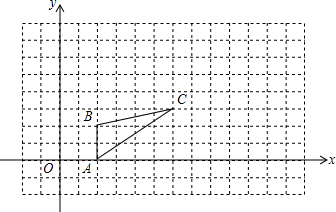 如图,图中的小方格都是边长为1的正方形,△ABC的A、B、C三点坐标为A(2,0)、B(2,2)、C(6,3).
如图,图中的小方格都是边长为1的正方形,△ABC的A、B、C三点坐标为A(2,0)、B(2,2)、C(6,3).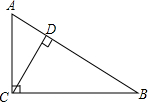 如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,则点C到AB的距离CD=$\frac{36}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,则点C到AB的距离CD=$\frac{36}{5}$.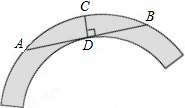 如图是一个圆环形黄花梨木摆件的残片,为求其外圆半径,小林在外圆上任取一点A,然后过点A作AB与残片的内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=15cm,AB=60cm,则这个摆件的外圆半径是37.5cm.
如图是一个圆环形黄花梨木摆件的残片,为求其外圆半径,小林在外圆上任取一点A,然后过点A作AB与残片的内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=15cm,AB=60cm,则这个摆件的外圆半径是37.5cm.