题目内容
7.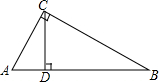 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=3,BD=6,求∠ACD的各个三角函数值.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=3,BD=6,求∠ACD的各个三角函数值.
分析 根据在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,可以得到∠ACD和∠BCD的关系,根据CD=3,BD=6,可以求得BC的长,从而可以求得∠B的各个三角函数值,从而可以求得∠ACD的各个三角函数值.
解答 解:∵在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=3,BD=6,
∴∠ACB=∠CDB=90°,∠ACD+∠DCB=∠DCB+∠B=90°,
∴∠ACD=∠B
∵∠CDB=90°,CD=3,BD=6,
∴$BC=\sqrt{C{D}^{2}+B{D}^{2}}=\sqrt{{3}^{2}+{6}^{2}}$=$\sqrt{45}=3\sqrt{5}$,
∴$sinB=\frac{CD}{BC}=\frac{3}{3\sqrt{5}}=\frac{\sqrt{5}}{5}$,$cosB=\frac{BD}{BC}=\frac{6}{3\sqrt{5}}=\frac{2\sqrt{5}}{5}$,$tanB=\frac{CD}{BD}=\frac{3}{6}=\frac{1}{2}$,
∴$sin∠ACD=\frac{\sqrt{5}}{5},cos∠ACD=\frac{2\sqrt{5}}{5}$,$tan∠ACD=\frac{1}{2}$,
即∠ACD的各个三角函数值分别是:$sin∠ACD=\frac{\sqrt{5}}{5},cos∠ACD=\frac{2\sqrt{5}}{5}$,$tan∠ACD=\frac{1}{2}$.
点评 本题考查解直角三角形,解题的关键是利用转化的数学思想将所求角的三角函数值转化可以求出的角的三角函数值,根据等角的三角函数值相等,即可解答所求的角的三角函数值.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
15.在Rt△ABC中,∠C=90°,CD是高,如果AD=m,∠A=α,那么BC的长为( )
| A. | m•tanα•cosα | B. | m•cotα•cosα | C. | $\frac{m•tanα}{cosα}$ | D. | $\frac{m•tanα}{sinα}$ |
1.已知(m-n)2=32,(m+n)2=4000,则m2+n2的值为( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 4032 |
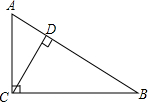 如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,则点C到AB的距离CD=$\frac{36}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,则点C到AB的距离CD=$\frac{36}{5}$.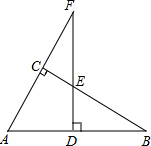 如图,在△ABC中,∠ACB=90°,点F在边AC的延长线上,且FD⊥AB,垂足为点D,如果AD=6,AB=10,ED=2,那么FD=12.
如图,在△ABC中,∠ACB=90°,点F在边AC的延长线上,且FD⊥AB,垂足为点D,如果AD=6,AB=10,ED=2,那么FD=12.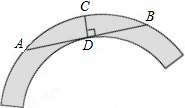 如图是一个圆环形黄花梨木摆件的残片,为求其外圆半径,小林在外圆上任取一点A,然后过点A作AB与残片的内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=15cm,AB=60cm,则这个摆件的外圆半径是37.5cm.
如图是一个圆环形黄花梨木摆件的残片,为求其外圆半径,小林在外圆上任取一点A,然后过点A作AB与残片的内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=15cm,AB=60cm,则这个摆件的外圆半径是37.5cm.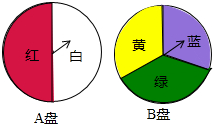 小颖为班级联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么配成了紫色.
小颖为班级联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么配成了紫色. 一个缺角的三角形残片如图所示,不恢复这个残角,你能否作出AB边上的高所在的直线?试说明理由.
一个缺角的三角形残片如图所示,不恢复这个残角,你能否作出AB边上的高所在的直线?试说明理由.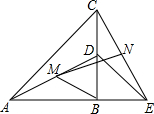 如图,点B为AE上一点,点D在BC上,AB=BC,BD=BE,∠ABC=90°,M、N分别是AD、CE的中点,求∠BMN的度数.
如图,点B为AE上一点,点D在BC上,AB=BC,BD=BE,∠ABC=90°,M、N分别是AD、CE的中点,求∠BMN的度数.