题目内容
10.如图,AB、BC、CD分别与⊙O切于A、E、D,CD∥AB,连接CO、BO;(1)求∠BOC的度数;
(2)若CO=3$\sqrt{5}$,BO=6$\sqrt{5}$,求⊙O的半径;
(3)在(2)的条件下,P为AD左侧圆上一点,PM∥CO交CD于M,PN∥BO交AB于N,当BN=2CM时,求线段DM的长度.
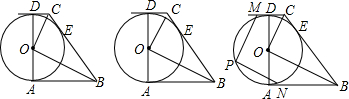
分析 (1)连接OE,根据切线的性质可得出∠DOC=∠COE,∠EOB=∠AOB,再由平角的定义即可得出结论;
(2)先根据勾股定理求出BC的长,再由面积法求出OE的长即可;
(3)延长CO交PN于K,过M作MQ⊥CO于Q,连OP可得出四边形MPKQ是矩形,根据勾股定理求出CD与AB的长,设DM=a,则CM=3+a,BN=6+2a,由PN∥BO得出△ANL∽△ABO,故可得出AL,根据AAS定理得出△MCQ≌△OLK,故MQ=OK=PK,根据等腰直角三角形的性质得出OK的长,由COS∠KOL=$\frac{OK}{OL}$=$\frac{OD}{OC}$即可得出结论.
解答 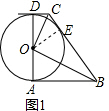 解:(1)如图1,连接OE,
解:(1)如图1,连接OE,
∵AB、BC、CD分别与⊙O切于A、E、D,
∴∠DOC=∠COE,∠EOB=∠AOB,
又∵∠DOC+∠COE+∠EOB+∠AOB=180°,
∴∠BOC=90°;
(2)∵CO=3$\sqrt{5}$,BO=6$\sqrt{5}$,∠BOC=90°,
∴BC=$\sqrt{{OC}^{2}+{OB}^{2}}$=$\sqrt{{(3\sqrt{5})}^{2}+{(6\sqrt{5})}^{2}}$=15.
∵OC•OB=BC•OE,
∴OE=$\frac{OC•OB}{BC}$=$\frac{3\sqrt{5}•6\sqrt{5}}{15}$=6,
∴⊙O的半径为6;
(3)如图2,延长CO交PN于K,过M作MQ⊥CO于Q,连OP,
∵PM∥CO,PN∥BO,
∴四边形MPKQ是矩形,
∴MQ=PK .
.
∵在Rt△OCD中,OD=6,OC=3$\sqrt{5}$,
∴CD=$\sqrt{{OC}^{2}-{OD}^{2}}$=$\sqrt{{(3\sqrt{5})}^{2}-{6}^{2}}$=3.
∵BN=2CM,
∴BN=6.
同理,在Rt△ABO中,
∵OB=6$\sqrt{5}$,OA=6,
∴AB=12.
设DM=a,则CM=3+a,BN=6+2a
∵AB=12,
∴AN=6-2a.
∵PN∥BO,
∴△ANL∽△ABO,
∴$\frac{AN}{AB}$=$\frac{AL}{OA}$,即$\frac{6-2a}{12}$=$\frac{AL}{6}$,解得AL=3-a,
∴OL=3+a,
∴OL=CM.
∵∠COD=∠KOL,∠COD=∠CMQ,
∴∠CMQ=∠KOL.
在△MCQ与△OLK中,
$\left\{\begin{array}{l}∠CMQ=∠LOK\\∠MQD=∠OKL\\ MC=OL\end{array}\right.$,
∴△MCQ≌△OLK(AAS),
∴MQ=OK=PK,
∴△OPK是等腰直角三角形,
∵OP=6,
∴OK=3$\sqrt{2}$,
∴COS∠KOL=$\frac{OK}{OL}$=$\frac{OD}{OC}$,即$\frac{3\sqrt{2}}{3+a}$=$\frac{6}{3\sqrt{5}}$,解得a=$\frac{3\sqrt{10}-6}{2}$,
∴DM=$\frac{3\sqrt{10}-6}{2}$.
点评 本题考查的是圆的综合题,涉及到切线的性质、全等三角形的判定与性质、相似三角形的判定与性质等知识,在解答(3)时要注意作出辅助线,构造出矩形及等腰直角三角形,利用勾股定求解.

 名校课堂系列答案
名校课堂系列答案 如图,两块直角三角板的直顶角O重合在一起,若∠BOC=$\frac{1}{5}$∠AOD,则∠BOC的度数为( )
如图,两块直角三角板的直顶角O重合在一起,若∠BOC=$\frac{1}{5}$∠AOD,则∠BOC的度数为( )| A. | 30° | B. | 45° | C. | 54° | D. | 60° |
| A. | m•tanα•cosα | B. | m•cotα•cosα | C. | $\frac{m•tanα}{cosα}$ | D. | $\frac{m•tanα}{sinα}$ |
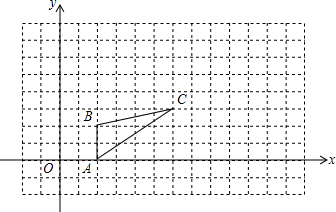 如图,图中的小方格都是边长为1的正方形,△ABC的A、B、C三点坐标为A(2,0)、B(2,2)、C(6,3).
如图,图中的小方格都是边长为1的正方形,△ABC的A、B、C三点坐标为A(2,0)、B(2,2)、C(6,3).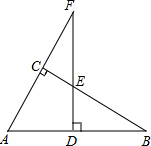 如图,在△ABC中,∠ACB=90°,点F在边AC的延长线上,且FD⊥AB,垂足为点D,如果AD=6,AB=10,ED=2,那么FD=12.
如图,在△ABC中,∠ACB=90°,点F在边AC的延长线上,且FD⊥AB,垂足为点D,如果AD=6,AB=10,ED=2,那么FD=12.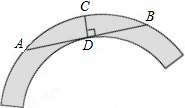 如图是一个圆环形黄花梨木摆件的残片,为求其外圆半径,小林在外圆上任取一点A,然后过点A作AB与残片的内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=15cm,AB=60cm,则这个摆件的外圆半径是37.5cm.
如图是一个圆环形黄花梨木摆件的残片,为求其外圆半径,小林在外圆上任取一点A,然后过点A作AB与残片的内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=15cm,AB=60cm,则这个摆件的外圆半径是37.5cm.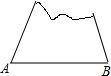 一个缺角的三角形残片如图所示,不恢复这个残角,你能否作出AB边上的高所在的直线?试说明理由.
一个缺角的三角形残片如图所示,不恢复这个残角,你能否作出AB边上的高所在的直线?试说明理由.