题目内容
10. 如图,AB为⊙O的直径,C为⊙O上一点,连AC、BC,E为⊙O上一点,且BE=CE,点F在BE上,CF⊥AB于D.
如图,AB为⊙O的直径,C为⊙O上一点,连AC、BC,E为⊙O上一点,且BE=CE,点F在BE上,CF⊥AB于D.(1)求证:CB=CF;
(2)若CF=2,EF=3,求BD的长.
分析 (1)由AB为⊙O的直径,得到∠ACB=90°,根据垂直的定义得到∠CDB=90°,根据余角的性质得到∠A=∠BCD,等量代换得到∠CFB=∠CBF,于是得到结论;
(2)根据相似三角形的性质得到BF=1,根据勾股定理即可得到结论.
解答 (1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∵CF⊥AB于D,
∴∠CDB=90°,
∴∠ACD+∠BCD=∠A+∠ACD=90°,
∴∠A=∠BCD,
∵∠A=∠E,
∴∠E=∠BCF,
∵CE=BD,
∴∠ECB=∠EBC,
∵∠ECB=∠ECF+∠BCF,
∠CFB=∠E+∠ECF,
∴∠CFB=∠CBF,
∴CB=CF;
解:(2)∵∠E=∠BCF,∠CBF=∠EBC,
∴△EBC∽△CBF
∴$\frac{BC}{BE}=\frac{BF}{BC}$,
∵CF=2,EF=3,
∴$\frac{2}{3+BF}=\frac{BF}{2}$,
∴BF=1,
∵BF2-DF2=BC2-CD2=BD2,
∴12-(2-CD)2=22-CD2,
∴CD=$\frac{7}{4}$,
∴BD=$\sqrt{4-(\frac{7}{4})^{2}}$=$\frac{\sqrt{15}}{4}$.
点评 本题考查了圆周角定理,相似三角形的判定和性质,勾股定理,等腰三角形的判定和性质,正确的识别图形是解题的关键.

练习册系列答案
相关题目
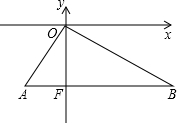 如图,在平面直角坐标系中,直角三角形的直角顶点与坐标原点重合,AB⊥y轴,垂足为点F,OA=2,∠B=30°,在Rt△OAB内(包含边界)有一动点M(x,y),以M为圆心的⊙M经过原点O,且与AB边相切于点C,⊙M与边OA、OB分别交于点D、E,则DE的取值范围为$\sqrt{3}$≤DE≤$\frac{4\sqrt{3}}{3}$.
如图,在平面直角坐标系中,直角三角形的直角顶点与坐标原点重合,AB⊥y轴,垂足为点F,OA=2,∠B=30°,在Rt△OAB内(包含边界)有一动点M(x,y),以M为圆心的⊙M经过原点O,且与AB边相切于点C,⊙M与边OA、OB分别交于点D、E,则DE的取值范围为$\sqrt{3}$≤DE≤$\frac{4\sqrt{3}}{3}$.