题目内容
2.对于正整数a,我们规定:若a为奇数,则f(a)=3a+1:若a为偶数,则f(a)=$\frac{a}{2}$,例如f(15)=3×15+1=46,f(10)=$\frac{10}{2}$=5,若a1=8,a2=f(a2),a3=f(a2),a4=f(a3),…,依此规律进行下去,得到一列数a1,a2,a3,a4,…,a${\;}_{2017}^{\;}$,…,则a1+a2+a3+a4+…+a2017=4712.分析 按照规定:若a为奇数,则f(a)=3a+1;若a为偶数,则f(a)=$\frac{a}{2}$,直接运算得出a2、a3、a4、a5、a6…,进一步找出规律解决问题.
解答 解:a1=8,a2=$\frac{8}{2}$=4,a3=$\frac{4}{2}$=2,a4=$\frac{2}{2}$=1,a5=1×3+1=4,a6=$\frac{4}{2}$=2,…,
这一列数按照除a1外,按照4、2、1三个数一循环,
∵2016÷3=672,
∴a1+a2+a3+…+a2014=8+(4+2+1)×672=8+4704=4712.
故答案为:4712.
点评 此题考查数列的规律,通过运算得出规律:这一列数按照除a1外,按照4、2、1三个数一循环是解题的关键.

练习册系列答案
相关题目
 如图,AB为⊙O的直径,C为⊙O上一点,连AC、BC,E为⊙O上一点,且BE=CE,点F在BE上,CF⊥AB于D.
如图,AB为⊙O的直径,C为⊙O上一点,连AC、BC,E为⊙O上一点,且BE=CE,点F在BE上,CF⊥AB于D.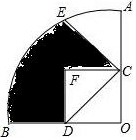 如图,在圆心角为90°的扇形AOB中,半径OA=2,点C、D分别是OA、OB的中点,点E是$\widehat{AB}$的一个三等分点,将△COD沿CD折叠,点O落在点F处,则图中阴影部分的面积为$\frac{2}{3}$π-$\frac{1}{2}$.
如图,在圆心角为90°的扇形AOB中,半径OA=2,点C、D分别是OA、OB的中点,点E是$\widehat{AB}$的一个三等分点,将△COD沿CD折叠,点O落在点F处,则图中阴影部分的面积为$\frac{2}{3}$π-$\frac{1}{2}$.