题目内容
18.已知关于x的一元二次方程x2+2(k+1)x+k2+2=0有两个实数根x1,x2.(1)求实数k的取值范围;
(2)若|x1|+|x2|=2$\sqrt{5}$,求k值.
分析 (1)由根的判别式即可得;
(2)由x1+x2=-2(k+1)<0,x1x2=k2+2>0知x1<0,x2<0,从而由|x1|+|x2|=2$\sqrt{5}$可得-(x1+x2)=2$\sqrt{5}$,代入求解即可.
解答 解:(1)∵方程由两个实数根,
∴△=4(k+1)2-4(k2+2)≥0,
解得:k≥$\frac{1}{2}$;
(2)∵x1+x2=-2(k+1)<0,x1x2=k2+2>0,
∴x1<0,x2<0,
∴由|x1|+|x2|=2$\sqrt{5}$可得-(x1+x2)=2$\sqrt{5}$,即2(k+1)=2$\sqrt{5}$,
解得:k=$\sqrt{5}$-1.
点评 本题主要考查根的判别式和韦达定理,熟练掌握根的判别式的值与根的个数得关系及韦达定理是解题的关键.

练习册系列答案
相关题目
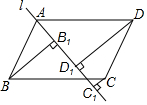 如图,过?ABCD的顶点A作直线l.
如图,过?ABCD的顶点A作直线l. 如图,AB为⊙O的直径,C为⊙O上一点,连AC、BC,E为⊙O上一点,且BE=CE,点F在BE上,CF⊥AB于D.
如图,AB为⊙O的直径,C为⊙O上一点,连AC、BC,E为⊙O上一点,且BE=CE,点F在BE上,CF⊥AB于D.