题目内容
5．已知实数a满足|2014-a|+$\sqrt{a-2015}$=a，那么a-20142+1的值是2016．分析 直接利用二次根式有意义的条件以及结合绝对值的性质将已知化简，进而求出答案．
解答 解：∵|2014-a|+$\sqrt{a-2015}$=a，
∴a≥0，且a-2015≥0，
解得：a≥2015，
故|2014-a|+$\sqrt{a-2015}$=a可化简为：
a-2104+$\sqrt{a-2015}$=a，
整理得：$\sqrt{a-2015}$=2014，
故a-2015=20142，
则a-20142+1=a-（a-2015）+1=2016．
故答案为：2016．
点评 此题主要考查了二次根式有意义的条件，正确化简已知等式是解题关键．
练习册系列答案
相关题目
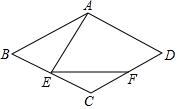如图，四边形ABCD为菱形，∠C=120°，点E是BC上一点．∠AEF=60°，EF交CD于F，求证：（1）∠BAE=∠CEF；（2）AE=EF．
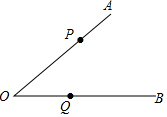已知点P、Q分别在∠ACB的边OA、OB上，按下列要求画图
如图，AB为⊙O的直径，C为⊙O上一点，连AC、BC，E为⊙O上一点，且BE=CE，点F在BE上，CF⊥AB于D．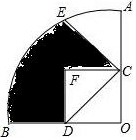
如图，在圆心角为90°的扇形AOB中，半径OA=2，点C、D分别是OA、OB的中点，点E是$\widehat{AB}$的一个三等分点，将△COD沿CD折叠，点O落在点F处，则图中阴影部分的面积为$\frac{2}{3}$π-$\frac{1}{2}$．
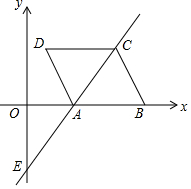已知：菱形ABCD在直角坐标系中的位置如图所示，与y轴交与点E的直线y=$\frac{3}{2}$x-3过点A和点C，且点A平分线段CE．