题目内容
11.四边形ABCD是菱形,点E在BC上,点F在AB上,点H在CD上,连接AE,FH交于点P,∠APF=∠ABC.(1)如图1,若∠ABC=90°,点F和点B重合,求证:AE=BH;
(2)如图2.求证:AE=FH;
(3)如图3,若AF+CH=BE,求∠B的度数.
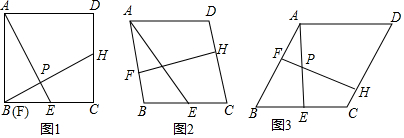
分析 (1)首先证明四边形ABCD是正方形,再证明△ABE≌△CBH即可.
(2)如图2中,延长CB到N,使得AN=AE,作HM∥BC交AB于M.则四边形ADHM是平行四边形,AD=HM,只要证明△ABN≌△HMF,即可解决问题.
(3)如图3中,在CB取一点N,使得AN=AE,作FM∥BC交CD于M.则四边形ADMF是平行四边形,AD=FM,AF=DM,由△ANB≌△AEC,推出AB=AC=BC,推出△ABC是等边三角形,由此即可解决问题.
解答 (1)证明:如图1中,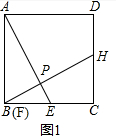
∵四边形ABCD是菱形,∠ABC=90°,
∴四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°,
∵∠APF=∠ABC=90°,
∴∠BAE+∠ABP=90°,∠ABP+∠CBH=90
∴∠BAE=∠CBH,
在△ABE和△BCH中,
$\left\{\begin{array}{l}{∠BAE=∠CBH}\\{AB=BC}\\{∠ABE=∠C}\end{array}\right.$,
∴△ABE≌△BCH,
∴AE=BH.
(2)证明:如图2中,延长CB到N,使得AN=AE,作HM∥BC交AB于M.
则四边形ADHM是平行四边形,AD=HM,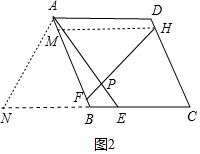
∵四边形ABCD是菱形,
∴AB=AD=HM,
∵HM∥CN,
∴∠HMF=∠ABN,
∵∠APF=∠ABC,∠PAF=∠BAE,
∴∠AFP=∠AEB=∠N,
∴△ABN≌△HMF,
∴AN=HF,
∵AE=AN,
∴AE=HF.
(3)解:如图3中,在CB取一点N,使得AN=AE,作FM∥BC交CD于M.
则四边形ADMF是平行四边形,AD=FM,AF=DM,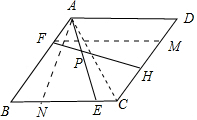
由(1)可知△ABN≌△FMH,
BN=HM,
∵BC=CD,AF+CH=DM+CH=BE,
∴CE=HM=BN,
在△ANB和△AEC中,
$\left\{\begin{array}{l}{AN=AE}\\{∠ANB=∠AEC}\\{BN=EC}\end{array}\right.$,
∴△ANB≌△AEC,
∴AB=AC=BC,
∴△ABC是等边三角形,
∴∠B=60°.
点评 本题考查菱形的性质、平行四边形的判定和性质、等边三角形的判定和性质,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

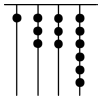 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )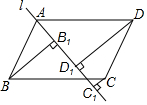 如图,过?ABCD的顶点A作直线l.
如图,过?ABCD的顶点A作直线l.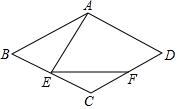 如图,四边形ABCD为菱形,∠C=120°,点E是BC上一点.∠AEF=60°,EF交CD于F,求证:(1)∠BAE=∠CEF;(2)AE=EF.
如图,四边形ABCD为菱形,∠C=120°,点E是BC上一点.∠AEF=60°,EF交CD于F,求证:(1)∠BAE=∠CEF;(2)AE=EF. 如图是某商品包装盒上的一个标签,你能从这个标签上看出这个商品的包装盒有多重、体积有多大吗?
如图是某商品包装盒上的一个标签,你能从这个标签上看出这个商品的包装盒有多重、体积有多大吗? 如图,AB为⊙O的直径,C为⊙O上一点,连AC、BC,E为⊙O上一点,且BE=CE,点F在BE上,CF⊥AB于D.
如图,AB为⊙O的直径,C为⊙O上一点,连AC、BC,E为⊙O上一点,且BE=CE,点F在BE上,CF⊥AB于D.