题目内容
(1)图①所示,在△ABC中,∠ABC的平分线与∠ACB的平分线相交于点O,试探究∠BOC与∠A的等量关系.
(2)图②所示,将∠ABC的一边BC延长至D,∠ABC的平分线与∠ACD的平分线相交于点O,试探究∠BOC与∠A的等量关系.
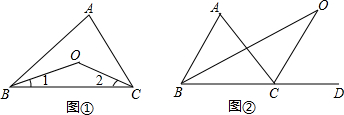
(2)图②所示,将∠ABC的一边BC延长至D,∠ABC的平分线与∠ACD的平分线相交于点O,试探究∠BOC与∠A的等量关系.

考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)先根据BO、CO分别是∠ABC、∠ACB的平分线得出∠1+∠2=
(180°-∠A),再根据∠1+∠2+∠BOC=180°即可得出结论;
(2)根据角平分线的定义得∠OBC=
∠ABC,∠OCD=
∠ACD,再根据三角形外角性质得∠ACD=∠A+∠ABC,∠OCD=∠OBC+∠BOC,所以
(∠A+∠ABC)=∠OBC+∠BOC=
∠ABC+∠BOC,然后整理可得∠BOC=
∠A.
| 1 |
| 2 |
(2)根据角平分线的定义得∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∠BOC=90°+
∠A.
∵BO、CO分别是∠ABC、∠ACB的平分线,
∴∠1+∠2=
(180°-∠A),
∴∠BOC=180°-(∠1+∠2)=180°-
(180°-∠A)=90°+
∠A;
(2)∵△ABC的内角平分线BO与外角平分线CO交于O,
∴∠OBC=
∠ABC,∠OCD=
∠ACD,
∵∠ACD=∠A+∠ABC,∠OCD=∠OBC+∠BOC,
∴
(∠A+∠ABC)=∠OBC+∠BOC=
∠ABC+∠BOC,
∴∠BOC=
∠A.
| 1 |
| 2 |
∵BO、CO分别是∠ABC、∠ACB的平分线,
∴∠1+∠2=
| 1 |
| 2 |
∴∠BOC=180°-(∠1+∠2)=180°-
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵△ABC的内角平分线BO与外角平分线CO交于O,
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ACD=∠A+∠ABC,∠OCD=∠OBC+∠BOC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=
| 1 |
| 2 |
点评:本题考查了三角形内角和定理,即三角形内角和是180°,也考查了三角形外角性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
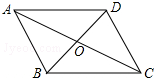 如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为23,则平行四边形ABCD的两条对角线的和是( )
如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为23,则平行四边形ABCD的两条对角线的和是( )| A、17 | B、27 | C、34 | D、44 |

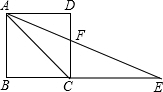 如图,点E在正方形ABCD的边BC的延长线上,且CE=CA,AE与CD交于F点,DF=
如图,点E在正方形ABCD的边BC的延长线上,且CE=CA,AE与CD交于F点,DF=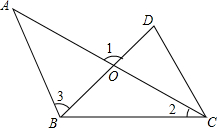 已知AB∥CD,AC平分∠BCD,∠2=35°,∠3=70°,求∠1的度数.
已知AB∥CD,AC平分∠BCD,∠2=35°,∠3=70°,求∠1的度数.