题目内容

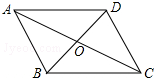如图，平行四边形ABCD的对角线交于点O，且AB=6，△OCD的周长为23，则平行四边形ABCD的两条对角线的和是（　　）
A、17B、27C、34D、44
考点：平行四边形的性质
专题：
分析：首先由平行四边形的性质可求出CD的长，由条件△OCD的周长为23，即可求出OD+OC的长，再根据平行四边的对角线互相平分即可求出平行四边形的两条对角线的和．
解答：解：∵四边形ABCD是平行四边形，
∴AB=CD=6，
∵△OCD的周长为23，
∴OD+OC=23-6=17，
∵BD=2DO，AC=2OC，
∴平行四边形ABCD的两条对角线的和=BD+AC=2（DO+OC）=34，
故选C．
点评：本题主要考查了平行四边形的基本性质，并利用性质解题．平行四边形的基本性质：①平行四边形两组对边分别平行；②平行四边形的两组对边分别相等；③平行四边形的两组对角分别相等；④平行四边形的对角线互相平分．
练习册系列答案
相关题目
（1）观察发现：
如图（1），已知直线m∥n，点A、B在直线n上，点C、P在直线m上，当点P在直线m上移动到任意一位置时，总有
 
与△ABC的面积相等．
（2）实践应用
①如图（2），在△ABC中，已知BC=6，且BC边上的高为5，若过C作CE∥AB，连接AE，BE，则△BAE的面积=
 
；
②如图（3），A、B、E三点在同一直线上，四边形ABCD和四边形BEFG都是邻边相等的平行四边形，若AB=5，AC=4，求△ACF的面积．
（3）拓展延伸
如图（4），在四边形ABCD中，AB与CD不平行，AB≠CD，且S△ABC＜S△ACD，过点A画一条直线平分四边形ABCD面积（简单介绍作法，不必说明理由）
（1）图①所示，在△ABC中，∠ABC的平分线与∠ACB的平分线相交于点O，试探究∠BOC与∠A的等量关系．
（2）图②所示，将∠ABC的一边BC延长至D，∠ABC的平分线与∠ACD的平分线相交于点O，试探究∠BOC与∠A的等量关系．
解方程：x3+3x2-6x=8．
用代数式表示：
（1）某品牌电脑按原售价降低m元后，又降低10%，现售价为a元，则电脑的原价是多少？
（2）某市出租车收费标准为：起步价8元，3千米后每千米加1.4元，则某人乘出租车s千米的付费是多少．
△ABC中，∠BAC=45°，S△ABC=12，BC=4，点D、E、F为BC、AB、AC边上的动点，则△DEF周长的最小值为
 
．
实验测得，从150cm高处自由下落的物体的下落时间t（s）与相应的高度h（m）、速度v（m/s）间的关系如下表：
t/s12345
v/（m/s）9.819.629.439.249
h/m145.1130.4105.971.627.5
v能看作t的一次函数吗？h呢？
如图，四边形ABCD中，AB=AD，BC边的垂直平分线MN经过点A，求证：点A在CD的垂直平分线上．
如图，在梯形ABCD中，AB∥CD，AD=BC，底角为a，以腰BC为直径作圆，与另一腰切于点M，交较长底边AB于点E，则
BE
AE
的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网