题目内容
（1）已知关于x、y的方程组
的解集满足不等式
求满足条件的m的整数值．
（2）描述证明：海宝在研究数学问题时发现了一个有趣的现象
①请你应数学表达式补充完整海宝发现的这个有趣的现象；
②请你证明海宝发现的这个有趣现象．
|
|
（2）描述证明：海宝在研究数学问题时发现了一个有趣的现象
①请你应数学表达式补充完整海宝发现的这个有趣的现象；
②请你证明海宝发现的这个有趣现象．
考点：二元一次方程组的解,分式的混合运算
专题：
分析：（1）首先根据方程组可得y=
，把y=
代入①得：x=m+
，然后再把x=m+
，y=
代入不等式组
中得
，再解不等式组，确定出整数解即可．
（2）①根据海宝的叙述，易得到规律为若
+
+2=ab，那么a+b=ab；
②首先将①式的等号左边通分、合并，此时分子是一个完全平方式，等号左右两边同乘以ab，可得到：（a+b）2=（ab）2，由于a、b均为正数，即可证得①的结论．
| 4 |
| 7 |
| 4 |
| 7 |
| 8 |
| 7 |
| 8 |
| 7 |
| 4 |
| 7 |
|
|
（2）①根据海宝的叙述，易得到规律为若
| a |
| b |
| b |
| a |
②首先将①式的等号左边通分、合并，此时分子是一个完全平方式，等号左右两边同乘以ab，可得到：（a+b）2=（ab）2，由于a、b均为正数，即可证得①的结论．
解答：（1）解：
，
①×2得：2x-4y=2m③，
②-③得：y=
，
把y=
代入①得：x=m+
，
把x=m+
，y=
代入不等式组
中得
，
解不等式组得：-4＜m≤-
，
则m=-3，-2．
（2）①解：若
+
+2=ab，那么a+b=ab；
②证明：∵
+
+2=ab，
∴
=ab，
∴a2+b2+2ab=（ab）2，
∴（a+b）2=（ab）2，
∵a＞0，b＞0，a+b＞0，ab＞0，
∴a+b=ab．
|
①×2得：2x-4y=2m③，
②-③得：y=
| 4 |
| 7 |
把y=
| 4 |
| 7 |
| 8 |
| 7 |
把x=m+
| 8 |
| 7 |
| 4 |
| 7 |
|
|
解不等式组得：-4＜m≤-
| 4 |
| 3 |
则m=-3，-2．
（2）①解：若
| a |
| b |
| b |
| a |
②证明：∵
| a |
| b |
| b |
| a |
∴
| a2+b2+2ab |
| ab |
∴a2+b2+2ab=（ab）2，
∴（a+b）2=（ab）2，
∵a＞0，b＞0，a+b＞0，ab＞0，
∴a+b=ab．
点评：（1）主要考查了一元一次不等式组的整数解，以及二元一次方程的解，关键是掌握消元的方法，用含m的式子表示x、y．
（2）主要考查的是分式的加减运算及完全平方公式的应用，通过图表形象地解决了数学知识．
（2）主要考查的是分式的加减运算及完全平方公式的应用，通过图表形象地解决了数学知识．
练习册系列答案
相关题目
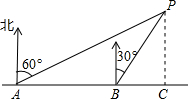如图，小明同学在东西方向的环海路A处，测得海中灯塔P在它的北偏东60°方向上，在A的正东400米的B处，测得海中灯塔P在它的北偏东30°方向上．问：灯塔P到环海路的距离PC约等于多少米？（
画出图中长方体的正投影．
