题目内容
在实数范围内定义运算“⊕”其法则为:a⊕b=a2b2,求方程(4⊕3)⊕x=24的解.
考点:解一元二次方程-直接开平方法
专题:新定义
分析:先根据新定义计算出4⊕3=144,则144⊕x=1442•x2,然后得到方程1442•x2=24,再利用直接开平方法解方程.
解答:解:∵4⊕3=42•32=144,
∴144⊕x=1442•x2,
∴1442•x2=24,
∴x2=
,
∴x=±
=±
,
∴x1=
,x2=-
.
∴144⊕x=1442•x2,
∴1442•x2=24,
∴x2=
| 24 |
| 1442 |
∴x=±
2
| ||
| 144 |
| ||
| 72 |
∴x1=
| ||
| 72 |
| ||
| 72 |
点评:本题考查了解一元二次方程-直接开平方法:形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解一元二次方程.

练习册系列答案
相关题目
 画出图中长方体的正投影.
画出图中长方体的正投影.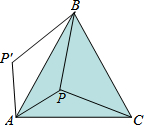 如图,P是正三角形ABC内一点,PA=5,PB=12,PC=13,若三角形PAC绕点A逆时针旋转后,得到三角形P′AB,则∠APB=
如图,P是正三角形ABC内一点,PA=5,PB=12,PC=13,若三角形PAC绕点A逆时针旋转后,得到三角形P′AB,则∠APB=
 如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D,试说明:AC∥DF,将过程补充完整.
如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D,试说明:AC∥DF,将过程补充完整.