题目内容
1.现有一个真命题:如图1,△ABC是等边三角形,被一平行于BC的矩形所截,如果E、F是AB的三分点,H、G是AC的三分点.那么重叠部分(即四边形EFGH)的面积是△ABC的$\frac{1}{3}$.(1)请你证明这个真命题;
(2)课题学习一:
①如果是任意三角形(如图2),判断结论是否成立,不必说明理由;
②如果是梯形(图3),结论是否成立,若成立,请加以证明;若不成立,不必说明理由;
(3)课题学习二:
①如果E、F是△ABC的边AB的五等分的第二,三等飞点,H、G是边AC的五等分的第二、三等分点(如图4)通过计算,直接写出四边形EFGH的面积与△ABC的面积的比值;
②如果E、F是△ABC的边AB的2n+1等分的第n、n+1的等分点,H、G是边AC的2n+1等分的第n、n+1等分点,猜想并直接写出四边形EFGH的面积与△ABC的面积的比值.

分析 (1)过点A作AM⊥BC于点M,交EH、FG于点N、P,设NP=m,则AM=3m,设EH=n,则BC=3n,FG=2n,根据$\frac{{S}_{四边形EFGH}}{{S}_{△ABC}}$=$\frac{\frac{1}{2}×(n+2n)m}{\frac{1}{2}×3n×3m}$进行化简即可;
(2)①如果是任意三角形,结论成立,证明过程同(1)相同;
②如果是梯形,过点A作AM⊥BC于点M,交EH、FG于点N、P,设NP=m,则AM=3m,设EH=a,BC=b,则FG=$\frac{1}{2}$(a+b),先求出AD=$\frac{3}{2}$a-$\frac{1}{2}$b,再根据$\frac{{S}_{四边形EFGH}}{{S}_{梯形ABCD}}$=$\frac{\frac{1}{2}[a+\frac{1}{2}(a+b)]•m}{\frac{1}{2}[(\frac{3}{2}a-\frac{1}{2}b)+b]•3m}$化简即可;
(3)过点A作AM⊥BC于点M,交EH、FG于点N、P.①设NP=m,则AM=5m,设EH=n,则BC=$\frac{5}{2}$n,FG=$\frac{3}{2}$n,根据$\frac{{S}_{四边形EFGH}}{{S}_{△ABC}}$=$\frac{\frac{1}{2}×(n+\frac{3}{2}n)m}{\frac{1}{2}×\frac{5}{2}n•5m}$化简即可;
②设NP=m,则AM=(2n+1)m,设EH=a,根据E、F是△ABC的边AB的2n+1等分的第n、n+1的等分点,H、G是边AC的2n+1等分的第n、n+1等分点,得出BC=$\frac{a(2n+1)}{n}$,FG=$\frac{a(n+1)}{n}$,再根据$\frac{{S}_{四边形EFGH}}{{S}_{△ABC}}$=$\frac{\frac{1}{2}×[a+\frac{a(n+1)}{n}]m}{\frac{1}{2}×\frac{a(2n+1)}{n}×(2n+1)m}$进行约分即可.
解答 解:(1)如图1: 过点A作AM⊥BC于点M,交EH、FG于点N、P,
过点A作AM⊥BC于点M,交EH、FG于点N、P,
设NP=m,则AM=3m,设EH=n,则BC=3n,FG=2n,
则$\frac{{S}_{四边形EFGH}}{{S}_{△ABC}}$=$\frac{\frac{1}{2}×(n+2n)m}{\frac{1}{2}×3n×3m}$=$\frac{1}{3}$;
(2)①如果是任意三角形,结论成立;
②如图2;如果是梯形,结论成立,
证明:过点A作AM⊥BC于点M,交EH、FG于点N、P,
设NP=m,则AM=3m,设EH=a,BC=b,则FG=$\frac{1}{2}$(a+b),
∵EH=$\frac{1}{2}$(AD+FG),
∴a=$\frac{1}{2}$[AD+$\frac{1}{2}$(a+b)],
∴AD=$\frac{3}{2}$a-$\frac{1}{2}$b,
∴$\frac{{S}_{四边形EFGH}}{{S}_{梯形ABCD}}$=$\frac{\frac{1}{2}[a+\frac{1}{2}(a+b)]•m}{\frac{1}{2}[(\frac{3}{2}a-\frac{1}{2}b)+b]•3m}$=$\frac{1}{3}$;
(3)如图3;过点A作AM⊥BC于点M,交EH、FG于点N、P,
①设NP=m,则AM=5m,设EH=n,则BC=$\frac{5}{2}$n,FG=$\frac{3}{2}$n,
则$\frac{{S}_{四边形EFGH}}{{S}_{△ABC}}$=$\frac{\frac{1}{2}×(n+\frac{3}{2}n)m}{\frac{1}{2}×\frac{5}{2}n•5m}$=$\frac{1}{5}$;
②设NP=m,则AM=(2n+1)m,设EH=a,
∵E、F是△ABC的边AB的2n+1等分的第n、n+1的等分点,H、G是边AC的2n+1等分的第n、n+1等分点,
∴$\frac{EH}{BC}$=$\frac{n}{2n+1}$,
∴BC=$\frac{a(2n+1)}{n}$,
∵$\frac{EG}{FG}$=$\frac{n}{n+1}$,
∴FG=$\frac{a(n+1)}{n}$,
∴$\frac{{S}_{四边形EFGH}}{{S}_{△ABC}}$=$\frac{\frac{1}{2}×[a+\frac{a(n+1)}{n}]m}{\frac{1}{2}×\frac{a(2n+1)}{n}×(2n+1)m}$=$\frac{1}{2n+1}$.
点评 此题考查了相似形综合,用到的知识点是相似三角形的性质与判定、平行线分线段成比例定理、三角形梯形的面积,关键是根据题意画出图形,作出辅助线.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案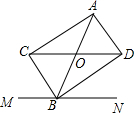 如图,点B在MN上,过AB的中点O作MN的平行线,分别交∠ABM的平分线和∠ABN的平分线于点C、D,求证:四边形ACBD是矩形.
如图,点B在MN上,过AB的中点O作MN的平行线,分别交∠ABM的平分线和∠ABN的平分线于点C、D,求证:四边形ACBD是矩形.
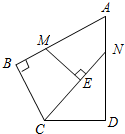 如图,在四边形ABCD中,AB=AD=3,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若BM:AM=AN:ND=1:2,ME⊥CN,则NE=$\frac{3\sqrt{7}}{7}$.
如图,在四边形ABCD中,AB=AD=3,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若BM:AM=AN:ND=1:2,ME⊥CN,则NE=$\frac{3\sqrt{7}}{7}$. 如图,已知△ABC.
如图,已知△ABC. 尺规作图:如图,已知∠α与线段a;求作:△ABC:使AB=AC=a,∠C=∠α(简要写出作法,保留作图痕迹).
尺规作图:如图,已知∠α与线段a;求作:△ABC:使AB=AC=a,∠C=∠α(简要写出作法,保留作图痕迹).