题目内容
13.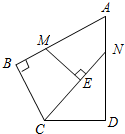 如图,在四边形ABCD中,AB=AD=3,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若BM:AM=AN:ND=1:2,ME⊥CN,则NE=$\frac{3\sqrt{7}}{7}$.
如图,在四边形ABCD中,AB=AD=3,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若BM:AM=AN:ND=1:2,ME⊥CN,则NE=$\frac{3\sqrt{7}}{7}$.
分析 连结AC,MC,MN,由条件可以得出△ACB≌△ACD,就可以得出∠BAC=∠DAC=30°,BC=DC,由勾股定理就可以求出AC、BC、CD、CN,再证明△BMC≌△NAM,就可以得出∠B=∠ANM=90°,设NE=x,由勾股定理建立方程就可以求出结论.
解答  解:连结AC,MC,MN,
解:连结AC,MC,MN,
∵AB⊥BC,AD⊥CD,
∴∠B=∠D=90°
在Rt△ACB和Rt△ACD中,
$\left\{\begin{array}{l}{AC=AC}\\{AB=AD}\end{array}\right.$,
∴Rt△ACB≌Rt△ACD(HL),
∴∠BAC=∠DAC,CB=CD.
∵∠BAD=60°,
∴∠BAC=∠DAC=30°,
∴AC=2BC.
∵AB2+BC2=AC2,AB=3,
∴9+BC2=4BC2,
∴BC=$\sqrt{3}$.
∴CD=$\sqrt{3}$.
∵BM:AM=AN:ND=1:2,
∴设BM=a,AM=2a,AN=b,DN=2b,
∴BM=1,AM=2,AN=1,DN=2,
在Rt△CBM和Rt△CDN中,由勾股定理,得
CM=2,CN=$\sqrt{7}$.
∴CM=2BM,
∴∠BCM=30°,
∴∠BMC=60°.
∴∠BMC=∠MAN,BM=NA,CM=MA.
在△BMC和△NAM中,
$\left\{\begin{array}{l}{BM=NA}\\{∠BMC=∠MAN}\\{CM=MA}\end{array}\right.$,
∴△BMC≌△NAM(SAS),
∴BC=NM=$\sqrt{3}$.
设NE为x,则CE=$\sqrt{7}-$x,
∴22-($\sqrt{7}$-x)2=($\sqrt{3}$)2-x2,
解得:x=$\frac{3\sqrt{7}}{7}$.
点评 本题考查了运用SAS,HL证明三角形全等的运用,全等三角形的性质的运用,比例的性质的运用,勾股定理的运用,解答时正确作辅助线是难点,证明三角形全等是关键.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案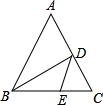 如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )
如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )| A. | AD<DE | B. | AD=DE | C. | AD>DE | D. | 不确定 |
| A. | 两条边对应相等 | B. | 一条边对应相等 | C. | 一锐角对应相等 | D. | 两锐角对应相等 |
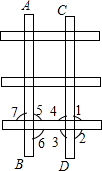 如图,在铺设铁轨时,两条铁轨必须是平行的,已知∠1是直角,那么再测量图中的哪个角(仅限图中已标出的角),就可以判断图中的两条铁轨AB、CD是否平行?为什么.
如图,在铺设铁轨时,两条铁轨必须是平行的,已知∠1是直角,那么再测量图中的哪个角(仅限图中已标出的角),就可以判断图中的两条铁轨AB、CD是否平行?为什么.
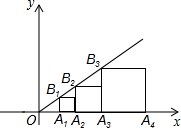 如图,直线y=$\frac{\sqrt{3}}{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以A1B1为边长,作正方形交x轴于A2,再过点A2作x轴的垂线交直线于点B2,以A2B2为边长作正方形交x轴于点A3,…,按此作法进行下去,则OA3的长为$\frac{4}{3}$+$\frac{2\sqrt{3}}{3}$.
如图,直线y=$\frac{\sqrt{3}}{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以A1B1为边长,作正方形交x轴于A2,再过点A2作x轴的垂线交直线于点B2,以A2B2为边长作正方形交x轴于点A3,…,按此作法进行下去,则OA3的长为$\frac{4}{3}$+$\frac{2\sqrt{3}}{3}$. 如图是一个正方形及其内切圆,随机地往正方形内投一粒米,落在圆内的概率为$\frac{π}{4}$.
如图是一个正方形及其内切圆,随机地往正方形内投一粒米,落在圆内的概率为$\frac{π}{4}$. A、B两种商品在一段时间内的销售总量如图所示:
A、B两种商品在一段时间内的销售总量如图所示: