题目内容
9．
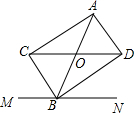如图，点B在MN上，过AB的中点O作MN的平行线，分别交∠ABM的平分线和∠ABN的平分线于点C、D，求证：四边形ACBD是矩形．
分析 根据角平分线定义和平行线推出∠OCB=∠OBC，推出OC=OB，同理OD=OB，即可得出答案．
解答 证明：∵CD平行MN，
∴∠OCB=∠CBM，
∵BC平分∠ABM，
∴∠OBC=∠CBM，
∴∠OCB=∠OBC，
∴OC=OB，
同理可证：OB=OD，
∴OA=OB=OC=OD，
∵CD=OC+OD，
AB=OA+OB，
∴AB=CD，
∴四边形ACBD是矩形（对角线互相平分且相等四边形是矩形）．
点评 本题考查了平行四边形的判定，矩形的判定，平行线的性质的应用，注意：对角线互相平分且相等四边形是矩形．
练习册系列答案
相关题目
