题目内容
15.已知$\sqrt{6n+4}$是整数,则正整数n的最小值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 因为$\sqrt{6n+4}$是整数,则(6n+4)是完全平方数,然后求满足条件的最小正整数n
解答 解:∵$\sqrt{6n+4}$是整数,
∴(6n+4)是完全平方数,且6n+4≥0,
∴n≥-$\frac{2}{3}$,
∴n的最小正整数值是2.
故选:A.
点评 考查了二次根式的定义.二次根式有意义的条件是被开方数是非负数.

练习册系列答案
相关题目
3. 如图所示,在矩形ABCD中,E是BC的中点,AE=AD=2,则AC的长是( )
如图所示,在矩形ABCD中,E是BC的中点,AE=AD=2,则AC的长是( )
 如图所示,在矩形ABCD中,E是BC的中点,AE=AD=2,则AC的长是( )
如图所示,在矩形ABCD中,E是BC的中点,AE=AD=2,则AC的长是( )| A. | $\sqrt{5}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | $\sqrt{7}$ |
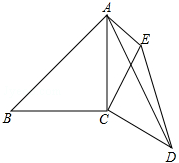 如图,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.
如图,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长. 如图,某飞机在空中A处探测到它的正下方地平面上目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角∠1为30°,则飞机A与指挥台B的距离为2400m.
如图,某飞机在空中A处探测到它的正下方地平面上目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角∠1为30°,则飞机A与指挥台B的距离为2400m.