题目内容
10.计算:(1)$2x{y^2}•({x^2}{y^3}-\frac{1}{4}{x^3}{y^2})$;
(2)(-2x-3y)(-2x+3y)-(3x-2y)2;
(3)(-16a5b4+8a4b5)÷(-2ab)3;
(4)${(-\frac{4}{3})^9}×{0.75^{10}}$+1(用简便方法计算).
分析 (1)根据乘法的分配律和同底数幂的乘法进行计算即可;
(2)根据平方差公式和完全平方公式展开再化简即可解答本题;
(3)根据同底数幂的除法进行化简即可;
(4)根据积的乘方进行化简即可解答本题.
解答 解:(1)$2x{y^2}•({x^2}{y^3}-\frac{1}{4}{x^3}{y^2})$
=$2{x^3}{y^5}-\frac{1}{2}{x^4}{y^4}$;
(2)(-2x-3y)(-2x+3y)-(3x-2y)2
=(4x2-9y2)-(9x2-12xy+4y2)
=4x2-9y2-9x2+12xy-4y2
=-5x2+12xy-13y2;
(3)(-16a5b4+8a4b5)÷(-2ab)3
=(-16a5b4+8a4b5)÷(-8a3b3)
=2a2b-ab2;
(4)${(-\frac{4}{3})^9}×{0.75^{10}}$+1
=${(-\frac{4}{3})^9}×{(\frac{3}{4})^{10}}+1$
=${(-\frac{4}{3}×\frac{3}{4})^9}×\frac{3}{4}+1$
=$-\frac{3}{4}+1$
=$\frac{1}{4}$.
点评 本题考查整式的混合运算,解题的关键是明确整式的混合运算的计算方法.

练习册系列答案
相关题目
5.若am=2,an=3,则am-n的值是( )
| A. | -1 | B. | 6 | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
15.已知$\sqrt{6n+4}$是整数,则正整数n的最小值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
20.下列函数中,为一次函数的是( )
| A. | $y=\frac{1}{x}+1$ | B. | y=-2x | C. | y=x2+1 | D. | y=kx+1(k是常数) |
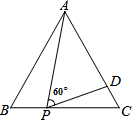 如图,等边三角形△ACB的边长为3,点P为BC上的一点,点D为AC上的一点,
如图,等边三角形△ACB的边长为3,点P为BC上的一点,点D为AC上的一点,