题目内容
6.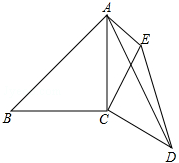 如图,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.
如图,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.
分析 连接BE,根据已知条件先证出∠BCE=∠ACD,根据SAS证出△ACD≌△BCE,得出AD=BE,再根据勾股定理求出AB,然后根据∠BAC=∠CAE=45°,求出∠BAE=90°,在Rt△BAE中,根据AB、AE的值,求出BE,从而得出AD.
解答 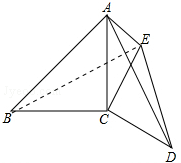 解:如图,连接BE,
解:如图,连接BE,
∵∠ACB=∠DCE=90°,
∴∠ACB+∠ACE=∠DCE+∠ACE,
即∠BCE=∠ACD,
又∵AC=BC,DC=EC,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠BCE=∠ACD}\\{DC=EC}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴AD=BE,
∵AC=BC=6,
∴AB=6$\sqrt{2}$,
∵∠BAC=∠CAE=45°,
∴∠BAE=90°,
在Rt△BAE中,AB=6$\sqrt{2}$,AE=3,
∴BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{(6\sqrt{2})^{2}+{3}^{2}}$=$\sqrt{81}$=9,
∴AD=9.
点评 此题考查了全等三角形的判定与性质,用到的知识点是全等三角形的判定与性质、勾股定理,关键是根据题意作出辅助线,证出△ACD≌△BCE.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.下列各图中,经过折叠能围成立方体的是( )
| A. | 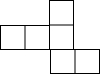 | B. | 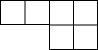 | C. | 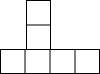 | D. | 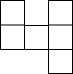 |
15.已知$\sqrt{6n+4}$是整数,则正整数n的最小值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 如图所示,已知线段MN,若用尺规作图作出MN的中点O,然后再作出OM的中点A,然后分别以O、A为圆心,以OM长为半径画弧,两弧交于点B,测量∠MBN的度数,结果为90°.
如图所示,已知线段MN,若用尺规作图作出MN的中点O,然后再作出OM的中点A,然后分别以O、A为圆心,以OM长为半径画弧,两弧交于点B,测量∠MBN的度数,结果为90°.