题目内容
6.已知x1,x2是关于x的方程k2x2+(2kb-4)x+b2=0的两个根,其中b≠0,且满足(k2十1)x1x2+kb(x1+x2)+b2=0.则$\frac{b}{k}$=4.分析 根据根与系数的关系得到x1+x2=-$\frac{2kb-4}{{k}^{2}}$,x1x2=$\frac{{b}^{2}}{{k}^{2}}$,代入(k2十1)x1x2+kb(x1+x2)+b2=0化简即可得到结论.
解答 解:∵x1,x2是关于x的方程k2x2+(2kb-4)x+b2=0的两个根,
∴x1+x2=-$\frac{2kb-4}{{k}^{2}}$,x1x2=$\frac{{b}^{2}}{{k}^{2}}$,
∴(k2十1)x1x2+kb(x1+x2)+b2=(k2+1)$•\frac{{b}^{2}}{{k}^{2}}$+kb•(-$\frac{2kb-4}{{k}^{2}}$)+b2=0,
∴(k2+1)•b-k(2kb-4)+b2k2=0,
∴b-4k=0,
∴$\frac{b}{k}$=4.
故答案为:4.
点评 本题考查了一元二次方程的根与系数的关系,熟记一元二次方程的根与系数的关系是解题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
14.下列各图中,经过折叠能围成立方体的是( )
| A. | 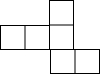 | B. | 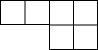 | C. | 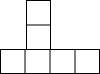 | D. | 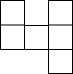 |
15.已知$\sqrt{6n+4}$是整数,则正整数n的最小值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |