题目内容
3. 如图所示,在矩形ABCD中,E是BC的中点,AE=AD=2,则AC的长是( )
如图所示,在矩形ABCD中,E是BC的中点,AE=AD=2,则AC的长是( )| A. | $\sqrt{5}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | $\sqrt{7}$ |
分析 由在矩形ABCD中,AE=AD=2,可得BC=2,又由E是BC的中点,求得BE的长,然后由勾股定理求得AB与AC的长.
解答 解:∵四边形ABCD是矩形,
∴∠B=90°,BC=AD=2,
∵E是BC的中点,
∴BE=$\frac{1}{2}$BC=1,
∵AE=2,
∴AB=$\sqrt{A{E}^{2}-B{E}^{2}}$=$\sqrt{3}$,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{7}$.
故选D.
点评 此题考查了勾股定理的应用以及矩形的性质.注意如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
14.下列各图中,经过折叠能围成立方体的是( )
| A. | 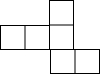 | B. | 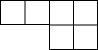 | C. | 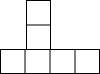 | D. | 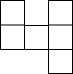 |
8.下列计算正确的是( )
| A. | 3a-a=3 | B. | a2+a3=a5 | C. | -(2a)3=-6a3 | D. | ab2÷a=b2 |
15.已知$\sqrt{6n+4}$是整数,则正整数n的最小值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
12.下列说法正确的是( )
| A. | -$\frac{x{y}^{2}}{5}$的系数是-5 | B. | 单项式x的系数为1,次数为0 | ||
| C. | xy+x次数为2次 | D. | -22xyz2的系数为6 |
 如图所示,已知线段MN,若用尺规作图作出MN的中点O,然后再作出OM的中点A,然后分别以O、A为圆心,以OM长为半径画弧,两弧交于点B,测量∠MBN的度数,结果为90°.
如图所示,已知线段MN,若用尺规作图作出MN的中点O,然后再作出OM的中点A,然后分别以O、A为圆心,以OM长为半径画弧,两弧交于点B,测量∠MBN的度数,结果为90°.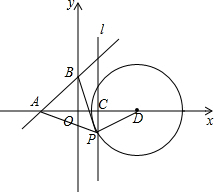 如图,直线y=x+b(b>0)与x、y轴分别相交于A、B两点,点C(1,0),过点C作垂直于x轴的直线l,在直线l上取一点P,满足PA=PB,点A关于直线l的对称点为点D,以D为圆心,DP为半径作⊙D.
如图,直线y=x+b(b>0)与x、y轴分别相交于A、B两点,点C(1,0),过点C作垂直于x轴的直线l,在直线l上取一点P,满足PA=PB,点A关于直线l的对称点为点D,以D为圆心,DP为半径作⊙D.