题目内容
4.甲乙两名同学解方程组 $\left\{\begin{array}{l}{x+ay=2}\\{bx-y=3}\end{array}\right.$.甲同学由于看错了系数a,得到方程组的解是$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$;由于乙同学看错了系数b,得到方程组的解是$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$.则a+b=5.分析 把甲的结果代入第二个方程,乙的结果代入第一个方程,求出a与b的值,即可求出a+b的值.
解答 解:把$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$代入bx-y=3中得:b+1=3,即b=2;
把$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$代入x+ay=2中得:-1+a=2,即a=3,
则a+b=2+3=5.
故答案为:5
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
14.下列各图中,经过折叠能围成立方体的是( )
| A. | 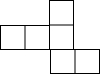 | B. | 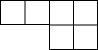 | C. | 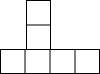 | D. | 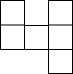 |
15.已知$\sqrt{6n+4}$是整数,则正整数n的最小值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
12.下列说法正确的是( )
| A. | -$\frac{x{y}^{2}}{5}$的系数是-5 | B. | 单项式x的系数为1,次数为0 | ||
| C. | xy+x次数为2次 | D. | -22xyz2的系数为6 |
14. 已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )
已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )
 已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )
已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )| A. | 外心 | B. | 内心 | C. | 重心 | D. | 无法确定 |
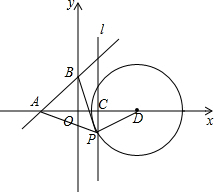 如图,直线y=x+b(b>0)与x、y轴分别相交于A、B两点,点C(1,0),过点C作垂直于x轴的直线l,在直线l上取一点P,满足PA=PB,点A关于直线l的对称点为点D,以D为圆心,DP为半径作⊙D.
如图,直线y=x+b(b>0)与x、y轴分别相交于A、B两点,点C(1,0),过点C作垂直于x轴的直线l,在直线l上取一点P,满足PA=PB,点A关于直线l的对称点为点D,以D为圆心,DP为半径作⊙D.