题目内容
2.如果关于x的方程x2-2(m+3)x+m2=0有两个不相等的实数根,那么m的取值范围是m>-$\frac{3}{2}$.分析 由方程有两个不相等的实数根结合根的判别式即可得出△=24m+36>0,解之即可得出m的取值范围.
解答 解:∵关于x的方程x2-2(m+3)x+m2=0有两个不相等的实数根,
∴△=[-2(m+3)]2-4m2=24m+36>0,
解得:m>-$\frac{3}{2}$.
故答案为:m>-$\frac{3}{2}$.
点评 本题考查了根的判别式,熟练掌握“当△>0时,方程有两个不相等的实数根”是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.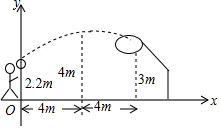 如图,一场篮球赛中,篮球运动员跳起投篮,已知球出手时离地面高2.2m,与篮圈中心的水平距离为8m,当球出手后水平距离为4m时达到最大高度4m,篮圈运行的轨迹为抛物线的一部分,篮圈中心距离地面3m,运动员发现未投中,若假设出手的角度和力度都不变,要使此球恰好通过篮圈中心,运动员应该跳得( )
如图,一场篮球赛中,篮球运动员跳起投篮,已知球出手时离地面高2.2m,与篮圈中心的水平距离为8m,当球出手后水平距离为4m时达到最大高度4m,篮圈运行的轨迹为抛物线的一部分,篮圈中心距离地面3m,运动员发现未投中,若假设出手的角度和力度都不变,要使此球恰好通过篮圈中心,运动员应该跳得( )
 如图,一场篮球赛中,篮球运动员跳起投篮,已知球出手时离地面高2.2m,与篮圈中心的水平距离为8m,当球出手后水平距离为4m时达到最大高度4m,篮圈运行的轨迹为抛物线的一部分,篮圈中心距离地面3m,运动员发现未投中,若假设出手的角度和力度都不变,要使此球恰好通过篮圈中心,运动员应该跳得( )
如图,一场篮球赛中,篮球运动员跳起投篮,已知球出手时离地面高2.2m,与篮圈中心的水平距离为8m,当球出手后水平距离为4m时达到最大高度4m,篮圈运行的轨迹为抛物线的一部分,篮圈中心距离地面3m,运动员发现未投中,若假设出手的角度和力度都不变,要使此球恰好通过篮圈中心,运动员应该跳得( )| A. | 比开始高0.8m | B. | 比开始高0.4m | C. | 比开始低0.8m | D. | 比开始低0.4m |
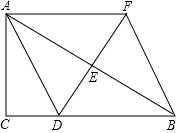 如图,在△ABC中,∠C=90°,点D为边BC上一点,点E为边AB的中点,过点A作AF∥BC,交DE的延长线于点F,联结BF.
如图,在△ABC中,∠C=90°,点D为边BC上一点,点E为边AB的中点,过点A作AF∥BC,交DE的延长线于点F,联结BF.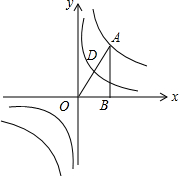 如图,反比例函数y=$\frac{8}{x}$的图象经过直角三角形OAB的顶点A,D为斜边OA的中点,则过点D的反比例函数的解析式为y=$\frac{2}{x}$.
如图,反比例函数y=$\frac{8}{x}$的图象经过直角三角形OAB的顶点A,D为斜边OA的中点,则过点D的反比例函数的解析式为y=$\frac{2}{x}$.