题目内容
7.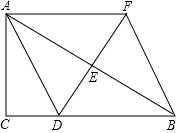 如图,在△ABC中,∠C=90°,点D为边BC上一点,点E为边AB的中点,过点A作AF∥BC,交DE的延长线于点F,联结BF.
如图,在△ABC中,∠C=90°,点D为边BC上一点,点E为边AB的中点,过点A作AF∥BC,交DE的延长线于点F,联结BF.(1)求证:四边形ADBF是平行四边形;
(2)当∠ADF=∠BDF时,求证:BD•BC=2BE2.
分析 (1)根据平行线的性质得到∠AFE=∠BDE,根据全等三角形的性质得到AF=BD,于是得到结论;
(2)根据已知条件得到?ADBF是菱形,根据菱形的性质得到AB⊥DF,根据相似三角形的性质即可得到结论.
解答 (1)证明:∵AF∥BC,
∴∠AFE=∠BDE,
在△AEF与△BED中,$\left\{\begin{array}{l}{∠AFE=∠BDE}\\{∠AEF=∠BED}\\{AE=BE}\end{array}\right.$,
∴△AEF≌△BED,
∴AF=BD,
∵AF∥BD,
∴四边形ADBF是平行四边形;
(2)解:∵∠ADF=∠BDF,
∴∠ADF=∠AFD,
∴AD=AF,
∴?ADBF是菱形,
∴AB⊥DF,
∴∠C=∠BED=90°,
∵∠ABC=∠DBE,
∴△ABC∽△DBE,
∴$\frac{BD}{AB}=\frac{BE}{BC}$,
∵AB=2BE,
∴BD•BC=2BE2.
点评 本题考查了相似三角形的判定和性质,平行四边形的判定,菱形的判定和性质,全等三角形的判定和性质,正确的识别图形是解题的关键.

练习册系列答案
相关题目
19.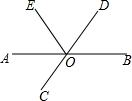 如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为( )
如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为( )
 如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为( )
如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
16.在-2,$\frac{1}{2}$,-3,6四个数中,最小的数是( )
| A. | -2 | B. | $\frac{1}{2}$ | C. | -3 | D. | 6 |
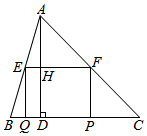 如图,在锐角△ABC中,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.
如图,在锐角△ABC中,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.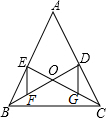 如图,△ABC的中线BD,CE相交于点O,点F,G分别是OB,OC的中点,则有EF∥DG,EF=DG,试说明理由.
如图,△ABC的中线BD,CE相交于点O,点F,G分别是OB,OC的中点,则有EF∥DG,EF=DG,试说明理由. 飞行员在空中观察地面的区域是一个圆(如图),当观察角α为50°,飞机的飞行高度h为9.8×102m时,观察区域的半径为多少米(结果精确到1m)?如果观察角度不变,要使观察区域面积增加1倍,那么飞机要升高多少米(精确到1m)?
飞行员在空中观察地面的区域是一个圆(如图),当观察角α为50°,飞机的飞行高度h为9.8×102m时,观察区域的半径为多少米(结果精确到1m)?如果观察角度不变,要使观察区域面积增加1倍,那么飞机要升高多少米(精确到1m)?