题目内容
10.若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=4,则△ABC的面积为8-4$\sqrt{3}$或8+4$\sqrt{3}$.分析 根据题意可以画出相应的图形,然后根据不同情况,求出相应的边的长度,从而可以求出不同情况下△ABC的面积.
解答 解:由题意可得,
当△ABC为△A1BC时,连接OB、OC,
∵点O是等腰△ABC的外心,且∠BOC=60°,底边BC=4,OB=OC,
∴△OBC为等边三角形,OB=OC=BC=4,OA1⊥BC于点D,
∴CD=2,
∴OD=$\sqrt{O{C}^{2}-C{D}^{2}}$=2$\sqrt{3}$,
∴A1D=4-2$\sqrt{3}$,
∴△ABC的面积=$\frac{1}{2}$×4×(4-2$\sqrt{3}$)=8-4$\sqrt{3}$,
当△ABC为△A2BC时,连接OB、OC,
A2D=4+2$\sqrt{3}$
同理可得,△ABC的面积=8+4$\sqrt{3}$,
故答案为:8-4$\sqrt{3}$或8+4$\sqrt{3}$.
点评 本题考查三角形的外接圆和外心,等腰三角形的性质,解题的关键是明确题意,找出所求问题需要的条件,利用分类讨论的数学思想解答问题.

练习册系列答案
相关题目
20.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费,设小红在同一商场累计购物x元,其中x>100.
(1)根据题题意,填写表格(单位:元)
(2)设小红在甲、乙两商场的实际花费分别为y1元、y2元,请分别写出y1、y2与x之间的关系式?
(3)小红选择哪家商场购物更合算?
(1)根据题题意,填写表格(单位:元)
| 累计购物 | 130 | 250 | … |
| 在甲商场 实际花费 | 100+(130-100)×90% | 100+(250-100)×90% | … |
| 在乙商场 实际花费 | 50+(130-50)×95% | 50+(250-50)×95% | … |
(3)小红选择哪家商场购物更合算?
5.某校社团活动课中,手工制作社的同学用一种彩色硬纸板制作某种长方体小礼品的包装盒,每张硬纸板可制作盒身12个,或制作盒底18个,1个盒身与2个盒底配成一套,现有42张这种彩色硬纸板,要使盒身和盒底刚好配套,若设需用x张做盒身,则下面所列方程正确的是( )
| A. | 18(42-x)=12x | B. | 2×18(42-x)=12x | C. | 18(42-x)=2×12x | D. | 18(21-x)=12x |
19.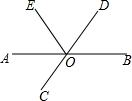 如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为( )
如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为( )
 如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为( )
如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
20.如图所示的四个几何体,其中左视图与俯视图相同的几何体共有几个( )

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
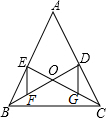 如图,△ABC的中线BD,CE相交于点O,点F,G分别是OB,OC的中点,则有EF∥DG,EF=DG,试说明理由.
如图,△ABC的中线BD,CE相交于点O,点F,G分别是OB,OC的中点,则有EF∥DG,EF=DG,试说明理由.