题目内容
12．已知$\left\{\begin{array}{l}{4x-3y-6z=0}\\{x+2y-7z=0}\end{array}\right.$，求$\frac{x-y+z}{x+y+z}$的值．分析 把z看做已知数表示出x与y，代入原式计算即可得到结果．
解答 解：方程组整理得：$\left\{\begin{array}{l}{4x-3y=6z①}\\{x+2y=7z②}\end{array}\right.$，
②×4-①得：11y=22z，即y=2z，
把y=2z代入②得：x=3z，
则原式=$\frac{3z-2z+z}{3z+2z+z}$=$\frac{1}{3}$．
点评 此题考查了解三元一次方程组，利用了消元的思想，用z表示出x与y是解本题的关键．
练习册系列答案
相关题目
20．如图所示的四个几何体，其中左视图与俯视图相同的几何体共有几个（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
己知：直线y=x+3与x轴、y轴分别交于点A、B，抛物线y=ax2+bx+c（a、b、c均不为0）与x轴交于点C、D两点．
飞行员在空中观察地面的区域是一个圆（如图），当观察角α为50°，飞机的飞行高度h为9.8×102m时，观察区域的半径为多少米（结果精确到1m）？如果观察角度不变，要使观察区域面积增加1倍，那么飞机要升高多少米（精确到1m）？
9．抛物线C1：y1=a1x2+b1x+c1中，函数值y1与自变量x之间的部分对应关系如下表：
（1）设抛物线C1的顶点为P，则点P的坐标为（-1，0）；
（2）现将抛物线C1沿x轴翻折，得到抛物线C2：y2=a2x2+b2x+c2，试求C2的解析式；
（3）现将抛物线C2向下平移，设抛物线在平移过程中，顶点为点D，与x轴的两交点为点A、B．
①在最初的状态下，至少向下平移多少个单位，点A、B之间的距离不小于6个单位？
②在最初的状态下，若向下平移m（m＞0）个单位时，对应的线段AB长为n，请直接写出m与n的等量关系．
| x | … | -3 | -2 | -1 | 1 | 3 | 4 | … |
| y1 | … | -4 | -1 | 0 | -4 | -16 | -25 | … |
（2）现将抛物线C1沿x轴翻折，得到抛物线C2：y2=a2x2+b2x+c2，试求C2的解析式；
（3）现将抛物线C2向下平移，设抛物线在平移过程中，顶点为点D，与x轴的两交点为点A、B．
①在最初的状态下，至少向下平移多少个单位，点A、B之间的距离不小于6个单位？
②在最初的状态下，若向下平移m（m＞0）个单位时，对应的线段AB长为n，请直接写出m与n的等量关系．
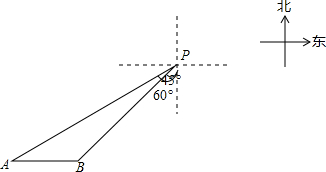一艘轮船位于灯塔P南偏西60°方向，距离灯塔200海里的A处，它向东航行多少海里到达灯塔P南偏西45°方向上的B处（参考数据：$\sqrt{3}$≈1.732，结果精确到0.1）？