题目内容
14.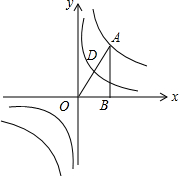 如图,反比例函数y=$\frac{8}{x}$的图象经过直角三角形OAB的顶点A,D为斜边OA的中点,则过点D的反比例函数的解析式为y=$\frac{2}{x}$.
如图,反比例函数y=$\frac{8}{x}$的图象经过直角三角形OAB的顶点A,D为斜边OA的中点,则过点D的反比例函数的解析式为y=$\frac{2}{x}$.
分析 过D作DM⊥x轴于M,根据三角形的中位线求出OM=$\frac{1}{2}$OB,DM=$\frac{1}{2}$AB,设A的坐标为(a,b),则M($\frac{1}{2}$a,$\frac{1}{2}$b),根据A在反比例函数y=$\frac{8}{x}$的图象上求出ab=8,即可求出答案.
解答 解: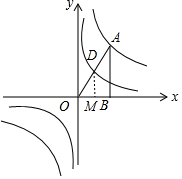
过D作DM⊥x轴于M,
∵直角三角形OAB,
∴∠ABO=∠DMO=90°,
∴AB∥DM,
∵D为OA的中点,
∴M为OB的中点,
∴OM=$\frac{1}{2}$OB,DM=$\frac{1}{2}$AB,
设A的坐标为(a,b),
则OM=$\frac{1}{2}$a,DM=$\frac{1}{2}$b,M($\frac{1}{2}$a,$\frac{1}{2}$b),
∵A在反比例函数y=$\frac{8}{x}$的图象上,
则ab=8,
∴$\frac{1}{2}$a•$\frac{1}{2}$b=2,
即过点D的反比例函数的解析式为y=$\frac{2}{x}$,
故答案为:y=$\frac{2}{x}$.
点评 本题考查了用待定系数法求出反比例函数的图象,直角三角形斜边上中线,三角形的中位线等知识点,能求出ab的值是解此题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
5.某校社团活动课中,手工制作社的同学用一种彩色硬纸板制作某种长方体小礼品的包装盒,每张硬纸板可制作盒身12个,或制作盒底18个,1个盒身与2个盒底配成一套,现有42张这种彩色硬纸板,要使盒身和盒底刚好配套,若设需用x张做盒身,则下面所列方程正确的是( )
| A. | 18(42-x)=12x | B. | 2×18(42-x)=12x | C. | 18(42-x)=2×12x | D. | 18(21-x)=12x |
19.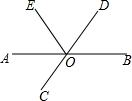 如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为( )
如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为( )
 如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为( )
如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
