题目内容
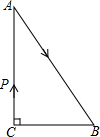 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒,问t为
如图,△ABC中,∠C=90°,AB=5cm,BC=3cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒,问t为考点:等腰三角形的判定
专题:动点型
分析:先根据勾股定理计算出AC=4cm,然后分类讨论:当CP=CB时,△BCP为等腰三角形,若点P在AC上得t=3(s),若点P在AB上,则t=5.4s;当PC=PB时,△BCP为等腰三角形,作PD⊥BC于D,如图,根据等腰三角形的性质得BD=CD,则可判断PD为△ABC的中位线,则AP=
AB=
,易得t=
(s);当BP=BC=3时,△BCP为等腰三角形,则AP=AB-BP=2,易得t=6(s).
| 1 |
| 2 |
| 5 |
| 2 |
| 13 |
| 2 |
解答:解:∵∠C=90°,AB=5cm,BC=3cm,
∴AC=
=4cm,
当CP=CB时,△BCP为等腰三角形,若点P在CA上,t=3(s);
若点P在AB上,CP=CB=3,作CH⊥AB于H,如图,CH=
,在Rt△BCH中,BH=
=
,
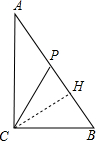
则PB=2BH=
,
∴CA+AP=4+5-
=5.4,此时t=5.4s;
当PC=PB时,△BCP为等腰三角形,作PD⊥BC于D,如图,
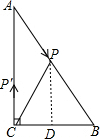
则BD=CD,
∴PD为△ABC的中位线,
∴AP=BP,即AP=
AB=
,
∴t=4+
=
(s);
当BP=BC时,△BCP为等腰三角形,即BP=BC=3,
∴AP=AB-BP=2,
∴t=4+2=6(s),
综上所述,t为3s或5s或6s或
s时,△BCP为等腰三角形.
故答案为3秒或5.4秒或6秒或
.
∴AC=
| AB2-BC2 |
当CP=CB时,△BCP为等腰三角形,若点P在CA上,t=3(s);
若点P在AB上,CP=CB=3,作CH⊥AB于H,如图,CH=
| 12 |
| 5 |
32-(
|
| 9 |
| 5 |

则PB=2BH=
| 18 |
| 5 |
∴CA+AP=4+5-
| 18 |
| 5 |
当PC=PB时,△BCP为等腰三角形,作PD⊥BC于D,如图,

则BD=CD,
∴PD为△ABC的中位线,
∴AP=BP,即AP=
| 1 |
| 2 |
| 5 |
| 2 |
∴t=4+
| 5 |
| 2 |
| 13 |
| 2 |
当BP=BC时,△BCP为等腰三角形,即BP=BC=3,
∴AP=AB-BP=2,
∴t=4+2=6(s),
综上所述,t为3s或5s或6s或
| 13 |
| 2 |
故答案为3秒或5.4秒或6秒或
| 13 |
| 2 |
点评:本题考查了等腰三角形的判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等.也考查了勾股定理和分类讨论的思想.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,∠D=∠AOD,若∠BAC=80°,则∠BCA的度数为
如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,∠D=∠AOD,若∠BAC=80°,则∠BCA的度数为 如图,已知△ABC中,BD平分∠ABC,CE=CD,DB=DE,∠E=30°.
如图,已知△ABC中,BD平分∠ABC,CE=CD,DB=DE,∠E=30°. 直线AB:y=-x+b分别与x,y轴交于A(8、0)、B两点,过点B的直线交x轴轴负半轴于C,且OB:OC=4:3
直线AB:y=-x+b分别与x,y轴交于A(8、0)、B两点,过点B的直线交x轴轴负半轴于C,且OB:OC=4:3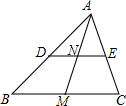 如图,△ABC中,AM是中线,点D、E分别在边AB、AC上,连接DE,且DE∥BC交AM于N,若DN=3,则DE=
如图,△ABC中,AM是中线,点D、E分别在边AB、AC上,连接DE,且DE∥BC交AM于N,若DN=3,则DE=