题目内容
已知∠AOB=3∠BOC,射线OD平分∠AOC,若∠BOD=20°,则∠BOC的度数为 .
考点:角平分线的定义
专题:
分析:根据题意先画出图形,分两种情况讨论∠BOC在∠AOB内部和∠BOC在∠AOB外部时,先根据∠AOB=3∠BOC,可设∠BOC=x,则∠AOB=3x,再根据角平分线的定义,将各个角用含有x的式子表示,最后根据∠BOD=20°,即可求出x的值,从而得出∠BOC的度数.
解答:解:如图1,当∠BOC在∠AOB内部时,

∵∠AOB=3∠BOC,
∴设∠BOC=x,则∠AOB=3x,
∴∠AOC=∠AOB-∠BOC=2x,
∵OD平分∠AOC,
∴∠DOC=
∠AOC=x,
∴∠BOD=∠DOC+∠BOC=2x,
∵∠BOD=20°,
∴2x=20°,
∴x=10°,
即∠BOC=10°;
如图2,当∠BOC在∠AOB外部时,

∵∠AOB=3∠BOC,
∴设∠BOC=x,则∠AOB=3x,
∴∠AOC=∠AOB+∠BOC=4x,
∵OD平分∠AOC,
∴∠DOC=
∠AOC=2x,
∴∠BOD=∠DOC-∠BOC=x,
∵∠BOD=20°,
∴x=20°,
即∠BOC=20°.
∴∠BOC的度数为:10°或20°.
故答案为:10°或20°.

∵∠AOB=3∠BOC,
∴设∠BOC=x,则∠AOB=3x,
∴∠AOC=∠AOB-∠BOC=2x,
∵OD平分∠AOC,
∴∠DOC=
| 1 |
| 2 |
∴∠BOD=∠DOC+∠BOC=2x,
∵∠BOD=20°,
∴2x=20°,
∴x=10°,
即∠BOC=10°;
如图2,当∠BOC在∠AOB外部时,

∵∠AOB=3∠BOC,
∴设∠BOC=x,则∠AOB=3x,
∴∠AOC=∠AOB+∠BOC=4x,
∵OD平分∠AOC,
∴∠DOC=
| 1 |
| 2 |
∴∠BOD=∠DOC-∠BOC=x,
∵∠BOD=20°,
∴x=20°,
即∠BOC=20°.
∴∠BOC的度数为:10°或20°.
故答案为:10°或20°.
点评:此题主要考查了角平分线的性质以及角的计算,根据已知画出相应的图形是本题的关键,注意有两种情况,不要漏解.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
能说明△ABC≌△DEF的条件是( )
| A、AB=DE,AC=DF,∠C=∠F |
| B、AC=EF,∠A=∠D,∠B=∠E |
| C、AB=DE,BC=EF,∠A=∠D |
| D、BC=EF,AB=DE,∠B=∠E |
 如图,在△ABC中,BC=2.点A的坐标是(-4,3),点B的坐标是(-3,1).
如图,在△ABC中,BC=2.点A的坐标是(-4,3),点B的坐标是(-3,1).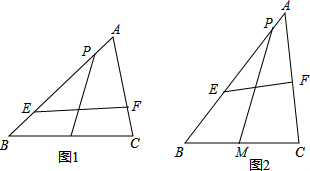
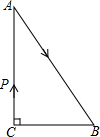 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒,问t为
如图,△ABC中,∠C=90°,AB=5cm,BC=3cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒,问t为