题目内容
解方程:
(1)3+|2x-1|=x
(2)3|x-1|-7=2
(3)|2x+1|=|x-3|
(4)10-5x=7(1-x)
(5)-(x-2)=2+x
(6)2(x-5)=3x+1.
(1)3+|2x-1|=x
(2)3|x-1|-7=2
(3)|2x+1|=|x-3|
(4)10-5x=7(1-x)
(5)-(x-2)=2+x
(6)2(x-5)=3x+1.
考点:含绝对值符号的一元一次方程,解一元一次方程
专题:
分析:(1)分类讨论:x<
,x≥
可化简去掉绝对值,根据解方程,可得答案;
(2)分类讨论:x<1,x≥1可化简去掉绝对值,根据解方程,可得答案;
(3)分类讨论:x<-
,-
≤x<3,x≥3,可化简去掉绝对值,根据解方程,可得答案;
(4)根据去括号、移项、合并同类项,系数化为1,可得方程的解;
(5)根据去括号、移项、合并同类项,系数化为1,可得方程的解;
(6)根据去括号、移项、合并同类项,系数化为1,可得方程的解.
| 1 |
| 2 |
| 1 |
| 2 |
(2)分类讨论:x<1,x≥1可化简去掉绝对值,根据解方程,可得答案;
(3)分类讨论:x<-
| 1 |
| 2 |
| 1 |
| 2 |
(4)根据去括号、移项、合并同类项,系数化为1,可得方程的解;
(5)根据去括号、移项、合并同类项,系数化为1,可得方程的解;
(6)根据去括号、移项、合并同类项,系数化为1,可得方程的解.
解答:解:(1)当x<
时,原方程等价于3+1-2x=x,解得x=
(不符合题意要舍去),
当x≥
时,原方程等价于3+2x-1=x,解得x=-2(不符合题意要舍去)
综上所述,原方程无解.
(2)当x<1时,原方程等价于-3x+3-7=2,解得x=-2,
当x>1时,原方程等价于,3x-3-7=2,解得x=4,
综上所述:x=-2或x=4.
(3)当x<-
时,原方程等价于-1-2x=3-x,解得x=-4;
当-
≤x<3时,原方程等价于1+2x=3-x,解得x=
;
当x≥3时,原方程等价于1+2x=x-3,解得x=-4(不符合题意要舍去),
综上所述:x=-4或x=
;
(4)去括号,得10-5x=7-7x,
移项,得-5x+7x=7-10,
合并同类项,得2x=-3
系数化为1,得x=-
;
(5)去括号,得-x+2=2+x,
移项,得-x-x=2-2,
合并同类项,得-2x=0
系数化为1,得x=0;
(6)去括号,得2x-10=3x+1,
移项,得2x-3x=1+10
合并同类项,得-x=11
系数化为1,得x=-11.
| 1 |
| 2 |
| 4 |
| 3 |
当x≥
| 1 |
| 2 |
综上所述,原方程无解.
(2)当x<1时,原方程等价于-3x+3-7=2,解得x=-2,
当x>1时,原方程等价于,3x-3-7=2,解得x=4,
综上所述:x=-2或x=4.
(3)当x<-
| 1 |
| 2 |
当-
| 1 |
| 2 |
| 2 |
| 3 |
当x≥3时,原方程等价于1+2x=x-3,解得x=-4(不符合题意要舍去),
综上所述:x=-4或x=
| 2 |
| 3 |
(4)去括号,得10-5x=7-7x,
移项,得-5x+7x=7-10,
合并同类项,得2x=-3
系数化为1,得x=-
| 3 |
| 2 |
(5)去括号,得-x+2=2+x,
移项,得-x-x=2-2,
合并同类项,得-2x=0
系数化为1,得x=0;
(6)去括号,得2x-10=3x+1,
移项,得2x-3x=1+10
合并同类项,得-x=11
系数化为1,得x=-11.
点评:本题考查了解含绝对值符号的一元一次方程,分类讨论是解题关键,去括号时要注意符号:括号前是正数去括号不变好,括号前是负数去括号全变号.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
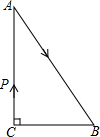 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒,问t为
如图,△ABC中,∠C=90°,AB=5cm,BC=3cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒,问t为 如图,已知A(3,0)、B(0,4),以A为顶点的抛物线与y轴交于点B.
如图,已知A(3,0)、B(0,4),以A为顶点的抛物线与y轴交于点B. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,联结DE,F为线段DE上一点,且∠AFE=∠B.若AB=5,AD=8,AE=4,则AF的长为
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,联结DE,F为线段DE上一点,且∠AFE=∠B.若AB=5,AD=8,AE=4,则AF的长为