题目内容
 如图,已知△ABC中,BD平分∠ABC,CE=CD,DB=DE,∠E=30°.
如图,已知△ABC中,BD平分∠ABC,CE=CD,DB=DE,∠E=30°.求证:△ABC是等边三角形.
考点:等边三角形的判定
专题:证明题
分析:根据等腰三角形的性质,由DB=DE得到∠DBC=∠E=30°,则∠ABC=2∠DBC=60°,再由CE=CD得到∠CDE=∠E=30°,于是利用三角形外角性质可计算出∠BCD=60°,接着根据三角形内角和计算出∠A=60°,即有∠A=∠ABC=∠ACB,然后根据等边三角形的判定可判断△ABC是等边三角形.
解答:证明:∵DB=DE,
∴∠DBC=∠E=30°,
∵BD平分∠ABC,
∴∠ABC=2∠DBC=60°,
∵CE=CD,
∴∠CDE=∠E=30°,
∴∠BCD=∠CDE+∠E=60°,
∴∠A=180°-∠ABC-∠ACB=60°,
∴∠A=∠ABC=∠ACB,
∴△ABC是等边三角形.
∴∠DBC=∠E=30°,
∵BD平分∠ABC,
∴∠ABC=2∠DBC=60°,
∵CE=CD,
∴∠CDE=∠E=30°,
∴∠BCD=∠CDE+∠E=60°,
∴∠A=180°-∠ABC-∠ACB=60°,
∴∠A=∠ABC=∠ACB,
∴△ABC是等边三角形.
点评:本题考查了等边三角形的判定:三条边都相等的三角形是等边三角形;三个角都相等的三角形是等边三角形;有一个角是60°的等腰三角形是等边三角形.也考查了等腰三角形的性质.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
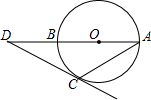 如图,AB是⊙O的直径,DC切⊙O于C,若∠A=25°,则∠D等于( )
如图,AB是⊙O的直径,DC切⊙O于C,若∠A=25°,则∠D等于( )| A、40° | B、50° |
| C、60° | D、70° |
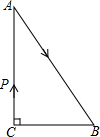 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒,问t为
如图,△ABC中,∠C=90°,AB=5cm,BC=3cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒,问t为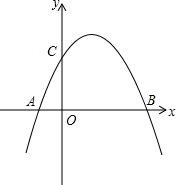 如图,抛物线y=
如图,抛物线y= 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y=
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y=