题目内容
14.在平面直角坐标系中,已知O是原点,四边形ABCD是长方形,A,B,C的坐标分别为A(-3,1),B(-3,3),C(2,3).(1)求D点坐标;
(2)将长方形ABCD以每秒1个单位长度的速度水平向右平移,2秒钟后所得的四边形A1B1C1D1四个顶点的坐标各是多少?
请将(1)(2)中的答案直接填入下表:
| 点 | D | A1 | B1 | C1 | D1 |
| 坐标 |
分析 (1)根据题意画出图形可得D点坐标;
(2)长方形ABCD以每秒1个单位长度的速度水平向右平移,2秒钟后向右平移了2个单位,把4个点的横坐标加上4即可;
(3)设x秒钟后△OBD的面积等于长方形ABCD的面积,表示出△OBD的各点坐标,再表示出△OBD的面积和长方形ABCD的面积可得方程,再解即可.
解答 解:(1)如图所示:点D的坐标为(2,1) ;
;
(2)
| 点 | D | A1 | B1 | C1 | D1 |
| 坐标 | (2,1) | (-1,1) | (-1,3) | (4,3) | (4,1) |
5×3-$\frac{1}{2}$×3×(3-x)-$\frac{1}{2}×$5×2-$\frac{1}{2}$×1×(2+x)=2×5,
解得:x=5.5,
答:5.5秒钟后△OBD的面积等于长方形ABCD的面积.
点评 此题主要考查了坐标与图形的变化,关键是掌握横坐标,右移加,左移减;纵坐标,上移加,下移减.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
5.已知a、b是一元二次方程x2-3x-2=0的两根,那么$\frac{1}{a}$+$\frac{1}{b}$的值为( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{3}{2}$ |
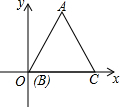 如图:正△ABC的边长为1,将一条长为2015的线段的一端固定在C处按CBAC…的规律紧绕在△ABC上,则线段的另一端点所在位置的坐标为($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
如图:正△ABC的边长为1,将一条长为2015的线段的一端固定在C处按CBAC…的规律紧绕在△ABC上,则线段的另一端点所在位置的坐标为($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).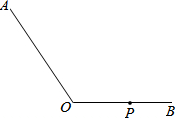 作图并填空:如图,在∠AOB中,点P在边OB上,
作图并填空:如图,在∠AOB中,点P在边OB上,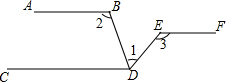 如图所示,已知AB∥CD∥EF,请问∠1、∠2、∠3之间有什么数量关系?请写出推理过程,并在每一步后面写上依据.
如图所示,已知AB∥CD∥EF,请问∠1、∠2、∠3之间有什么数量关系?请写出推理过程,并在每一步后面写上依据.