题目内容
9.(1)解方程组:$\left\{\begin{array}{l}{\frac{x}{2}+\frac{y}{3}=2①}\\{4x-y=5②}\end{array}\right.$(2)解不等式组:$\left\{\begin{array}{l}{x+2>0}\\{2(x+1)≥3x-1}\end{array}\right.$,并在数轴上表示它的解集.
分析 (1)首先去分母化简方程组,然后用加减消元法,把关于x和y的二元一次方程组转换为y的一元一次方程,再求解.
(2)根据不等式的性质求出不等式的解集,根据找不等式组解集的规律找出即可.
解答 (1)解:$\left\{\begin{array}{l}{\frac{x}{2}+\frac{y}{3}=2①}\\{4x-y=5②}\end{array}\right.$,
①×3得:$\frac{3}{2}$x+y=6③,
②+③得:$\frac{11}{2}$x=11,
∴x=2,
把x=2代入②,得4×2-y=5,
∴y=3,
∴原方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$.
(2)解:$\left\{\begin{array}{l}{x+2>0①}\\{2(x+1)≥3x-1②}\end{array}\right.$
解不等式①得 x>-2,
解不等式②得 x≤3
∴不等式组的解集为-2<x≤3;
∴原不等式组的解集在数轴上表示如图所示
点评 本题主要考查二元一次方程组的解法以及解一元一次不等式(组),掌握二元一次方程组的两种解法-加减消元法和代入消元法,能根据不等式的解集找出不等式组的解集是解题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
17.在平面直角坐标系中,已知线段AB的两个端点分别是A(-4,-1),B(1,1),将线段AB平移后得到线段A′B′,若点A′的坐标为(-2,3),则点B′的坐标为( )
| A. | (-1,5) | B. | (3,5) | C. | (3,-3) | D. | (-1,-3) |
14.将直线y=3x-2平移后,得到直线y=3x+6,则原直线( )
| A. | 沿y轴向上平移了8个单位 | B. | 沿y轴向下平移了8个单位 | ||
| C. | 沿x轴向左平移了8个单位 | D. | 沿x轴向右平移了8个单位 |
1.下列调查中,适宜采用全面调查方式的是( )
| A. | 旅客上飞机前的安全检查 | |
| B. | 对广州市七年级学生身高现状的调查 | |
| C. | 多某品牌食品安全的调查 | |
| D. | 对一批灯管使用寿命的调查 |
19.下列图案中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
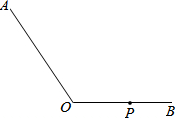 作图并填空:如图,在∠AOB中,点P在边OB上,
作图并填空:如图,在∠AOB中,点P在边OB上,