题目内容
11.实验学校计划阻值共青团员372人到某爱国主义基地接受教育,并安排8位老师同行,经学校与汽车出租公司协商,有两种型号客车可供选择,它们的载客量和租金如表所示,为了保证每人都有座位,学校决定租8辆车.(1)写出符合要求的租车方案,并说明理由;
(2)设租甲种客车x辆,总租金共y(元),写出y与x之间的函数关系式;
(3)在(1)的方案中,求出租金最少的租车方案.
| 车种 人数与租金 单位 | 甲种客车 | 乙种客车 |
| 载客量(单位:人/辆) | 50 | 30 |
| 租金(单位:元/辆) | 400 | 200 |
分析 (1)设甲种客车为x辆,本题的不等式关系为:甲种客车载客量+乙种车载客量≥372+8,根据“学校决定租用客车8辆”我们可知,甲种客车车应该在0-10辆的范围内,由此可得出不等式组进行求解,最后根据得出的自变量的取值范围,判定出符合条件的自变量的值.
(2)根据租金总额=租用甲种客车用的钱+租用乙种用的钱,即可解答;
(3)得出函数关系后根据(1)的自变量的取值范围和函数的性质判断出租金最少的方案.
解答 解:(1)设甲种客车为x辆,根据题意得,
$\left\{\begin{array}{l}{50x+30(8-x)≥372+8}\\{0≤x≤8}\end{array}\right.$,
解得:7≤x≤8,
又因为车辆数只能取整数,
所以x=7,8,
租车方案共2种.
①租甲种客车7辆,乙种客车1辆;
②租甲种客车8辆.
(2)y=400x+200(8-x)=200x+1600;
(3)y=400x+200(8-x)=200x+1600(7≤x≤8)
∵k=200>0,
∴y随x的增大而增大.
∴x取7时,y最小.
y=200×7+1600=3000(元).
答:租甲种客车7辆,乙种1辆时租金最少,租金为3000元.
点评 解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系.准确的解不等式是需要掌握的基本计算能力,要熟练掌握利用自变量的取值范围求最值的方法.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
1.下列调查中,适宜采用全面调查方式的是( )
| A. | 旅客上飞机前的安全检查 | |
| B. | 对广州市七年级学生身高现状的调查 | |
| C. | 多某品牌食品安全的调查 | |
| D. | 对一批灯管使用寿命的调查 |
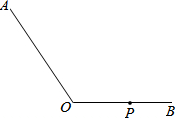 作图并填空:如图,在∠AOB中,点P在边OB上,
作图并填空:如图,在∠AOB中,点P在边OB上,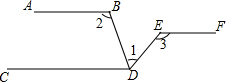 如图所示,已知AB∥CD∥EF,请问∠1、∠2、∠3之间有什么数量关系?请写出推理过程,并在每一步后面写上依据.
如图所示,已知AB∥CD∥EF,请问∠1、∠2、∠3之间有什么数量关系?请写出推理过程,并在每一步后面写上依据.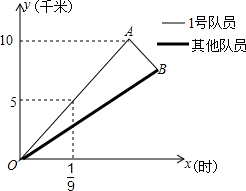 自行车队点的一次训练中,1号队员以高于其他队员10千米/时的速度独自前行,匀速行进一段时间后,又返回队伍,在往返过程中速度保持不变,设分开后行进的时间为x小时,1号队员和其他队员行进的路程分别为y1、y2(千米),且y1、y2与x的函数关系如图所示.
自行车队点的一次训练中,1号队员以高于其他队员10千米/时的速度独自前行,匀速行进一段时间后,又返回队伍,在往返过程中速度保持不变,设分开后行进的时间为x小时,1号队员和其他队员行进的路程分别为y1、y2(千米),且y1、y2与x的函数关系如图所示.