题目内容
8．
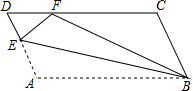如图，平行四边形ABCD中，点E在AD上，以BE为折痕，把△ABE向上翻折，点A正好落在CD边的点F处．若△FDE的周长为6，平行四边形ABCD的周长为26，那么CF的长为7．
分析 根据翻折变换的性质、平行四边形的性质证明AD+DC=AB+BC=13，运用△FDE的周长为6，可知AD+DF=6，求出FC的长即可．
解答 解：如图，∵四边形ABCD为平行四边形，
∴AD=BC，AB=DC；
由题意得：AE=FE，AB=BF；
∵平行四边形ABCD的周长为26，
∴AD+DC=AB+BC=13，
∵△FDE的周长为6，
∴DE+DF+EF=AD+DF=6，
∴FC=13-6=7．
故答案为7．
点评 该题主要考查了翻折变换的性质、平行四边形的性质等几何知识，解题的方法是准确找出图形中隐含的等量关系．灵活运用翻折变换的性质、平行四边形的性质是解题的关键．
练习册系列答案
相关题目
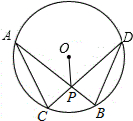如图，在⊙O中，弦AB、CD相交于点P，若AB=CD，∠APO=65°，则∠APC=50 度．
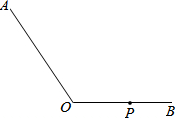作图并填空：如图，在∠AOB中，点P在边OB上，
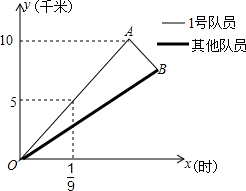自行车队点的一次训练中，1号队员以高于其他队员10千米/时的速度独自前行，匀速行进一段时间后，又返回队伍，在往返过程中速度保持不变，设分开后行进的时间为x小时，1号队员和其他队员行进的路程分别为y1、y2（千米），且y1、y2与x的函数关系如图所示．
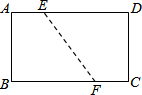如图，在矩形ABCD中，AB=6，BC=8，若将矩形折叠，使B点与D点重合，则折痕EF的长为7.5．
17．在平面直角坐标系中，已知线段AB的两个端点分别是A（-4，-1），B（1，1），将线段AB平移后得到线段A′B′，若点A′的坐标为（-2，3），则点B′的坐标为（ ）
| A． | （-1，5） | B． | （3，5） | C． | （3，-3） | D． | （-1，-3） |