题目内容
4.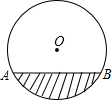 如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水的最大深度为2cm,则该输水管的半径为( )
如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水的最大深度为2cm,则该输水管的半径为( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
分析 先过点O作OD⊥AB于点D,连接OA,由垂径定理可知AD=$\frac{1}{2}$AB,设OA=r,则OD=r-2,在Rt△AOD中,利用勾股定理即可求出r的值.
解答  解:如图所示:过点O作OD⊥AB于点D,连接OA,
解:如图所示:过点O作OD⊥AB于点D,连接OA,
∵OD⊥AB,
∴AD=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4cm,
设OA=r,则OD=r-2,
在Rt△AOD中,OA2=OD2+AD2,即r2=(r-2)2+42,
解得r=5cm.
∴该输水管的半径为5cm;
故选C.
点评 本题考查的是垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
15.某班进行个人投篮比赛,受污染的表记录了在规定时间内投进n个球的人数分布情况,同时,已知进球3个或3个以上的人平均每人投进3.5个球,进球4个或4个以下的人平均每人投进2.5个球,问投进3个球和4个球的各有多少人?
| 进球数n | 0 | 1 | 2 | 3 | 4 | 5 |
| 投进n个球的人数 | 1 | 2 | 7 | 9 | 3 | 2 |
12.一个多边形的内角和是1620°,那么这个多边形是( )
| A. | 八边形 | B. | 九边形 | C. | 十边形 | D. | 十一边形 |
9.如果把多边形的边数增加一倍.得到的新多边形的内角和是1440°,那么原来多边形的边数是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
 如图所示,有一个二级台阶,每一级的长宽、高分别为60cm、45cm、27cm,A和B是这两个台阶的相对端点,A点上有一只蚂蚁想到B点去吃可口的食物.若蚂蚁平均每秒走0.8cm,则蚂蚁沿着台阶从A到B至少需要多少时间?
如图所示,有一个二级台阶,每一级的长宽、高分别为60cm、45cm、27cm,A和B是这两个台阶的相对端点,A点上有一只蚂蚁想到B点去吃可口的食物.若蚂蚁平均每秒走0.8cm,则蚂蚁沿着台阶从A到B至少需要多少时间?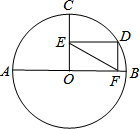 如图,⊙O的半径OC⊥AB,D为$\widehat{BC}$上一点,DE⊥OC,DF⊥AB,垂足分别为E、F,EF=3,求直径AB的长.
如图,⊙O的半径OC⊥AB,D为$\widehat{BC}$上一点,DE⊥OC,DF⊥AB,垂足分别为E、F,EF=3,求直径AB的长.