题目内容
16.计算:|$\frac{1}{2}-1$|+|$\frac{1}{3}-\frac{1}{2}$|+|$\frac{1}{4}-\frac{1}{3}$|+…+|$\frac{1}{100}-\frac{1}{99}$|的结果为$\frac{99}{100}$.分析 利用绝对值的意义,去掉绝对值,再进一步抵消计算得出答案即可.
解答 解:原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$+…+$\frac{1}{99}$-$\frac{1}{100}$
=1-$\frac{1}{100}$
=$\frac{99}{100}$.
故答案为:$\frac{99}{100}$.
点评 此题考查有理数的加减混合运算,绝对值的意义,利用绝对值的意义化简是解决问题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
6.数学应用:在“课内比教学”活动中,16位评委给吴老师的讲课比赛平分都在90分左右,把吴老师的得分超过或不足90分的部分分别用正、负数表示(单位:分),统计如下表:
(1)吴老师一共得了多少分?
(2)比赛选手得分计算方法:先去掉一个最高分,去掉一个最低分,然后计算出平均分,按此计算,吴老师的讲课比赛得分是多少?
| 超过或不足90分的部分 | -5 | -2.5 | -1 | 0 | 0.5 | 2 | 3 | 6 |
| 评委人数 | 2 | 2 | 3 | 4 | 2 | 1 | 1 | 1 |
(2)比赛选手得分计算方法:先去掉一个最高分,去掉一个最低分,然后计算出平均分,按此计算,吴老师的讲课比赛得分是多少?
4.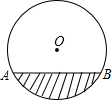 如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水的最大深度为2cm,则该输水管的半径为( )
如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水的最大深度为2cm,则该输水管的半径为( )
 如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水的最大深度为2cm,则该输水管的半径为( )
如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水的最大深度为2cm,则该输水管的半径为( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
8.已知三角形两个内角的差等于第三个内角,则它是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等边三角形 |
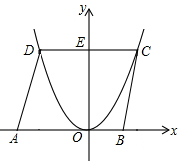 如图所示,已知函数y=ax2(a≠0)的图象上的点D,C与x轴上的点A(-5,0)和B(3,0)构成平行四边形ABCD,DC与y轴的交点为E(0,6),试求a的值.
如图所示,已知函数y=ax2(a≠0)的图象上的点D,C与x轴上的点A(-5,0)和B(3,0)构成平行四边形ABCD,DC与y轴的交点为E(0,6),试求a的值.