题目内容
15.某班进行个人投篮比赛,受污染的表记录了在规定时间内投进n个球的人数分布情况,同时,已知进球3个或3个以上的人平均每人投进3.5个球,进球4个或4个以下的人平均每人投进2.5个球,问投进3个球和4个球的各有多少人?| 进球数n | 0 | 1 | 2 | 3 | 4 | 5 |
| 投进n个球的人数 | 1 | 2 | 7 | 9 | 3 | 2 |
分析 设投进3个球的有x人,投进4个球的有y人,根据进球3个或3个以上的人平均每人投进3.5个球,进球4个或4个以下的人平均每人投进2.5个球,列方程组求解.
解答 解:设投进3个球的有x人,投进4个球的有y人.依题意得.
$\left\{\begin{array}{l}{3x+4y+5×2=3.5×(x+y+2)\\;}\\{2×1+7×2+3x+4y=2.5×(1+2+7+x+y)}\end{array}\right.$,
整理得$\left\{\begin{array}{l}{x-y=6}\\{x+3y=18}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=9}\\{y=3}\end{array}\right.$.
答:投进3个球的有9人,投进4个球的有3人.
故答案为9,3.
点评 本题考查了加权平均数以及二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
6.数学应用:在“课内比教学”活动中,16位评委给吴老师的讲课比赛平分都在90分左右,把吴老师的得分超过或不足90分的部分分别用正、负数表示(单位:分),统计如下表:
(1)吴老师一共得了多少分?
(2)比赛选手得分计算方法:先去掉一个最高分,去掉一个最低分,然后计算出平均分,按此计算,吴老师的讲课比赛得分是多少?
| 超过或不足90分的部分 | -5 | -2.5 | -1 | 0 | 0.5 | 2 | 3 | 6 |
| 评委人数 | 2 | 2 | 3 | 4 | 2 | 1 | 1 | 1 |
(2)比赛选手得分计算方法:先去掉一个最高分,去掉一个最低分,然后计算出平均分,按此计算,吴老师的讲课比赛得分是多少?
10.下列各数:$\frac{π}{2}$,0,$\sqrt{9}$,$\frac{1}{2}$,$0.\stackrel{••}{23}$,$\frac{22}{7}$,0.30003000…,1-$\sqrt{2}$中,无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
4.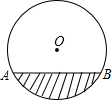 如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水的最大深度为2cm,则该输水管的半径为( )
如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水的最大深度为2cm,则该输水管的半径为( )
 如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水的最大深度为2cm,则该输水管的半径为( )
如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水的最大深度为2cm,则该输水管的半径为( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
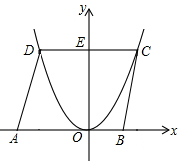 如图所示,已知函数y=ax2(a≠0)的图象上的点D,C与x轴上的点A(-5,0)和B(3,0)构成平行四边形ABCD,DC与y轴的交点为E(0,6),试求a的值.
如图所示,已知函数y=ax2(a≠0)的图象上的点D,C与x轴上的点A(-5,0)和B(3,0)构成平行四边形ABCD,DC与y轴的交点为E(0,6),试求a的值.