题目内容
14. 如图所示,有一个二级台阶,每一级的长宽、高分别为60cm、45cm、27cm,A和B是这两个台阶的相对端点,A点上有一只蚂蚁想到B点去吃可口的食物.若蚂蚁平均每秒走0.8cm,则蚂蚁沿着台阶从A到B至少需要多少时间?
如图所示,有一个二级台阶,每一级的长宽、高分别为60cm、45cm、27cm,A和B是这两个台阶的相对端点,A点上有一只蚂蚁想到B点去吃可口的食物.若蚂蚁平均每秒走0.8cm,则蚂蚁沿着台阶从A到B至少需要多少时间?
分析 根据题意画出台阶的侧面展开图,根据勾股定理求出AB的长,再由蚂蚁平均每秒走0.8cm即可得出结论.
解答  解:如图所示,
解:如图所示,
AB=$\sqrt{{60}^{2}+(45+27+45+27)^{2}}$=12$\sqrt{17}$(cm).
∵蚂蚁平均每秒走0.8cm,
∴$\frac{12\sqrt{17}}{0.8}$=15$\sqrt{17}$(秒).
答:蚂蚁沿着台阶从A到B至少需要15$\sqrt{17}$秒.
点评 本题考查的是平面展开-最短路径问题,根据题意画出圆柱的侧面展开图,利用勾股定理求解是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.数学应用:在“课内比教学”活动中,16位评委给吴老师的讲课比赛平分都在90分左右,把吴老师的得分超过或不足90分的部分分别用正、负数表示(单位:分),统计如下表:
(1)吴老师一共得了多少分?
(2)比赛选手得分计算方法:先去掉一个最高分,去掉一个最低分,然后计算出平均分,按此计算,吴老师的讲课比赛得分是多少?
| 超过或不足90分的部分 | -5 | -2.5 | -1 | 0 | 0.5 | 2 | 3 | 6 |
| 评委人数 | 2 | 2 | 3 | 4 | 2 | 1 | 1 | 1 |
(2)比赛选手得分计算方法:先去掉一个最高分,去掉一个最低分,然后计算出平均分,按此计算,吴老师的讲课比赛得分是多少?
4.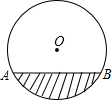 如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水的最大深度为2cm,则该输水管的半径为( )
如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水的最大深度为2cm,则该输水管的半径为( )
 如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水的最大深度为2cm,则该输水管的半径为( )
如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水的最大深度为2cm,则该输水管的半径为( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
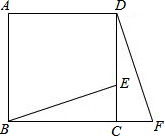 如图,E为正方形ABCD的边CD上一点,F为BC边延长线上一点,且有BE=DF,试判断BE与DF的位置关系.
如图,E为正方形ABCD的边CD上一点,F为BC边延长线上一点,且有BE=DF,试判断BE与DF的位置关系. 如图,斜坡AB的坡度为1:5,该段斜坡的长度为60m,求坡顶B点的垂直高度.
如图,斜坡AB的坡度为1:5,该段斜坡的长度为60m,求坡顶B点的垂直高度. 如图,在同一平面直角坐标系中画出函数y=$\frac{1}{2}$x2和y=2x2的图象
如图,在同一平面直角坐标系中画出函数y=$\frac{1}{2}$x2和y=2x2的图象