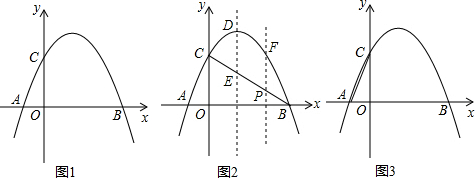
题目内容
15.关于二次函数y=x2-2x+1-a2图象,以下判断错误的是( )| A. | 开口方向确定 | B. | 对称轴位置确定 | ||
| C. | 与y轴的交点一定在正半轴 | D. | 与x轴的交点一定有一个在正半轴 |
分析 由二次函数y=x2-2x+1-a2,可得其对称轴;由二次项系数,可知图象开口向下;由二次项系数和一次项系数可知抛物线与x轴的交点的位置,对每个选项分析、判断即可.
解答 解:A、由二次函数y=x2-2x+1-a2得,a=1>0,开口向下;故本项错误;
B、由二次函数y=x2-2x+1-a2得,对称轴是x=1;故本项错误;
C、由二次函数y=x2-2x+1-a2可知,与y轴的交点坐标为(0,1-a2),1-a2无法求得符号,故本项正确;
D、由二次函数y=x2-2x+1-a2可知-$\frac{b}{a}$=-$\frac{-2}{1}$=2,所以与x轴的交点一定有一个在正半轴;故本项错误;
故选C.
点评 本题主要考查了二次函数的性质,应熟练掌握二次函数的性质:顶点、对称轴的求法及图象的特点.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
6.下列说法中,错误的是( )
| A. | 菱形的对角线互相平分 | B. | 正方形的对角线互相垂直平分 | ||
| C. | 矩形的对角线相等且平分 | D. | 平行四边形的对角线相等且垂直 |
5. 如图,岛P位于岛Q的正西方,P、Q两岛间的距离为20(1+$\sqrt{3}$)海里,由岛P、Q分别测得船R位于南偏东60°和南偏西45°方向上,则船R到岛P的距离为( )
如图,岛P位于岛Q的正西方,P、Q两岛间的距离为20(1+$\sqrt{3}$)海里,由岛P、Q分别测得船R位于南偏东60°和南偏西45°方向上,则船R到岛P的距离为( )
 如图,岛P位于岛Q的正西方,P、Q两岛间的距离为20(1+$\sqrt{3}$)海里,由岛P、Q分别测得船R位于南偏东60°和南偏西45°方向上,则船R到岛P的距离为( )
如图,岛P位于岛Q的正西方,P、Q两岛间的距离为20(1+$\sqrt{3}$)海里,由岛P、Q分别测得船R位于南偏东60°和南偏西45°方向上,则船R到岛P的距离为( )| A. | 40海里 | B. | 40$\sqrt{2}$海里 | C. | 40$\sqrt{3}$海里 | D. | 40$\sqrt{6}$海里 |
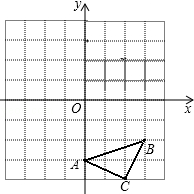 已知:如图△ABC三个顶点的坐标分别为A(0,-3)、B(3,-2)、C(2,-4),正方形网格中,每个小正方形的边长是1个单位长度.
已知:如图△ABC三个顶点的坐标分别为A(0,-3)、B(3,-2)、C(2,-4),正方形网格中,每个小正方形的边长是1个单位长度. 阅读下面材料:
阅读下面材料: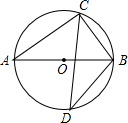 如图所示,在⊙O中,AB为⊙O的直径,AC=8,sinD=$\frac{3}{5}$,则BC=6.
如图所示,在⊙O中,AB为⊙O的直径,AC=8,sinD=$\frac{3}{5}$,则BC=6.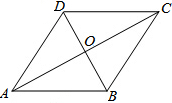 如图,菱形ABCD中,点O是对角线AC、BD的交点,已知AB=5,OB=3,则菱形ABCD的面积是24.
如图,菱形ABCD中,点O是对角线AC、BD的交点,已知AB=5,OB=3,则菱形ABCD的面积是24.