题目内容
19.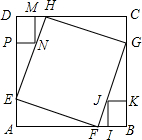 正方形ABCD的边长为12,在其角上去掉两个全等的矩形DMNP和矩形BIJK,DM=IB=2,DP=BK=3,正方形EFGH顶点分别在正方形ABCD的边上,且EH过N点,则正方形EFGH的边长是( )
正方形ABCD的边长为12,在其角上去掉两个全等的矩形DMNP和矩形BIJK,DM=IB=2,DP=BK=3,正方形EFGH顶点分别在正方形ABCD的边上,且EH过N点,则正方形EFGH的边长是( )| A. | 10 | B. | 3$\sqrt{10}$ | C. | 4$\sqrt{5}$ | D. | 3$\sqrt{10}$或4$\sqrt{5}$ |
分析 根据正方形的性质和平行线分线段的性质解答即可.
解答 解:设EP=x,可得HC=DE=x+3,DH=12-x-3=9-x,
因为PN∥DH,
可得:$\frac{2}{9-x}=\frac{x}{x+3}$,
解得:x1=1,x2=6,
当x=1时,EH=4$\sqrt{5}$,
当x=6时,EH=3$\sqrt{10}$,
故选:D
点评 此题考查正方形的性质,关键是根据正方形的性质和平行线分线段的性质解答.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
9.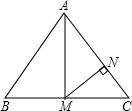 如图在△ABC中,AB=AC=10,BC=12,点M为BC的中点,MN⊥AC于点N,则MN等于( )
如图在△ABC中,AB=AC=10,BC=12,点M为BC的中点,MN⊥AC于点N,则MN等于( )
 如图在△ABC中,AB=AC=10,BC=12,点M为BC的中点,MN⊥AC于点N,则MN等于( )
如图在△ABC中,AB=AC=10,BC=12,点M为BC的中点,MN⊥AC于点N,则MN等于( )| A. | $\frac{12}{5}$ | B. | $\frac{18}{5}$ | C. | $\frac{24}{5}$ | D. | $\frac{32}{5}$ |
11. 如图是二次函数y=ax2+bx+c(a≠0)的图象,有下列判断:①2a+b=0;②当-1≤x≤3时,y≤0;③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,其中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)的图象,有下列判断:①2a+b=0;②当-1≤x≤3时,y≤0;③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,其中正确的是( )
 如图是二次函数y=ax2+bx+c(a≠0)的图象,有下列判断:①2a+b=0;②当-1≤x≤3时,y≤0;③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,其中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)的图象,有下列判断:①2a+b=0;②当-1≤x≤3时,y≤0;③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,其中正确的是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
8.下列四个实数中最大的是( )
| A. | -5 | B. | 0 | C. | $\sqrt{8}$ | D. | 3 |
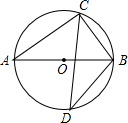 如图所示,在⊙O中,AB为⊙O的直径,AC=8,sinD=$\frac{3}{5}$,则BC=6.
如图所示,在⊙O中,AB为⊙O的直径,AC=8,sinD=$\frac{3}{5}$,则BC=6.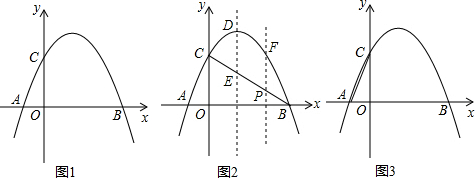
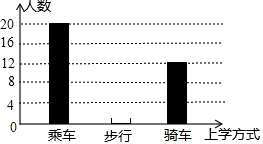 学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计,他通过采集数据后,绘制一幅不完整的统计图(如图所示).已知骑车的人数占全班人数的30%,结合图中提供的信息,可得该班步行上学的有8人.
学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计,他通过采集数据后,绘制一幅不完整的统计图(如图所示).已知骑车的人数占全班人数的30%,结合图中提供的信息,可得该班步行上学的有8人.