题目内容
14.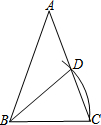 如图,在△ABC中,AB=AC,∠A=36°,以B为圆心,BC为半径作弧,交AC于点D,连接BD,则∠ABD=36°.
如图,在△ABC中,AB=AC,∠A=36°,以B为圆心,BC为半径作弧,交AC于点D,连接BD,则∠ABD=36°.
分析 在△ABC中可求得∠ACB=∠ABC=72°,在△BCD中可求得∠DBC=36°,可求出∠ABD.
解答 解:∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°,
又∵BC=BD,
∴∠BDC=∠BCD=72°,
∴∠DBC=36°,
∴∠ABD=∠ABC-∠DBC=72°-36°=36°,
故答案为:36
点评 本题主要考查等腰三角形的性质,掌握等边对等角是解题的关键,注意三角形内角和定理的应用.

练习册系列答案
相关题目
2.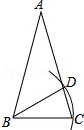 如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )
如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )
 如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )
如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )| A. | 30° | B. | 60° | C. | 45° | D. | 90° |
9.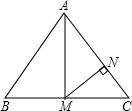 如图在△ABC中,AB=AC=10,BC=12,点M为BC的中点,MN⊥AC于点N,则MN等于( )
如图在△ABC中,AB=AC=10,BC=12,点M为BC的中点,MN⊥AC于点N,则MN等于( )
 如图在△ABC中,AB=AC=10,BC=12,点M为BC的中点,MN⊥AC于点N,则MN等于( )
如图在△ABC中,AB=AC=10,BC=12,点M为BC的中点,MN⊥AC于点N,则MN等于( )| A. | $\frac{12}{5}$ | B. | $\frac{18}{5}$ | C. | $\frac{24}{5}$ | D. | $\frac{32}{5}$ |
6.下列说法中,错误的是( )
| A. | 菱形的对角线互相平分 | B. | 正方形的对角线互相垂直平分 | ||
| C. | 矩形的对角线相等且平分 | D. | 平行四边形的对角线相等且垂直 |
 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=32°,则∠2的度数为28°.
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=32°,则∠2的度数为28°.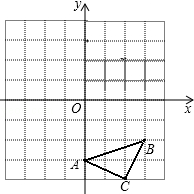 已知:如图△ABC三个顶点的坐标分别为A(0,-3)、B(3,-2)、C(2,-4),正方形网格中,每个小正方形的边长是1个单位长度.
已知:如图△ABC三个顶点的坐标分别为A(0,-3)、B(3,-2)、C(2,-4),正方形网格中,每个小正方形的边长是1个单位长度.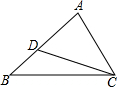 如图,在△ABC中,AB=10,AC=8,点D在边AB上,若∠ACD=∠B,则AD的长为6.4.
如图,在△ABC中,AB=10,AC=8,点D在边AB上,若∠ACD=∠B,则AD的长为6.4. 阅读下面材料:
阅读下面材料: