题目内容
14.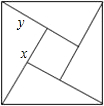 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
分析 由题意$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=49}&{①}\\{(x-y)^{2}=4}&{②}\end{array}\right.$,①-②可得2xy=45记为③,①+③得到(x+y)2=94由此即可判断.
解答 解:由题意$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=49}&{①}\\{(x-y)^{2}=4}&{②}\end{array}\right.$,
①-②得2xy=45 ③,
∴2xy+4=49,
①+③得x2+2xy+y2=94,
∴(x+y)2=94,
∴①②③正确,④错误.
故选B
点评 本题考查勾股定理,二元二次方程组等知识,解题的关键学会利用方程的思想解决问题,学会整体恒等变形的思想,属于中考常考题型.

练习册系列答案
相关题目
5. 如图,岛P位于岛Q的正西方,P、Q两岛间的距离为20(1+$\sqrt{3}$)海里,由岛P、Q分别测得船R位于南偏东60°和南偏西45°方向上,则船R到岛P的距离为( )
如图,岛P位于岛Q的正西方,P、Q两岛间的距离为20(1+$\sqrt{3}$)海里,由岛P、Q分别测得船R位于南偏东60°和南偏西45°方向上,则船R到岛P的距离为( )
 如图,岛P位于岛Q的正西方,P、Q两岛间的距离为20(1+$\sqrt{3}$)海里,由岛P、Q分别测得船R位于南偏东60°和南偏西45°方向上,则船R到岛P的距离为( )
如图,岛P位于岛Q的正西方,P、Q两岛间的距离为20(1+$\sqrt{3}$)海里,由岛P、Q分别测得船R位于南偏东60°和南偏西45°方向上,则船R到岛P的距离为( )| A. | 40海里 | B. | 40$\sqrt{2}$海里 | C. | 40$\sqrt{3}$海里 | D. | 40$\sqrt{6}$海里 |
2.下列的几何图形中,一定是轴对称图形的有( )
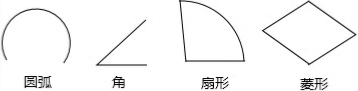

| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
19.如果等式x3•xm=x6成立,那么m=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
6.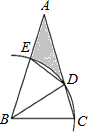 如图,△ABC中,∠A=30°,AB=AC,BC=2,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E,则线段AE、AD与$\widehat{DE}$围成的阴影部分的面积是 ( )
如图,△ABC中,∠A=30°,AB=AC,BC=2,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E,则线段AE、AD与$\widehat{DE}$围成的阴影部分的面积是 ( )
 如图,△ABC中,∠A=30°,AB=AC,BC=2,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E,则线段AE、AD与$\widehat{DE}$围成的阴影部分的面积是 ( )
如图,△ABC中,∠A=30°,AB=AC,BC=2,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E,则线段AE、AD与$\widehat{DE}$围成的阴影部分的面积是 ( )| A. | 2$\sqrt{3}$+2-$\frac{5}{6}$π | B. | $\sqrt{3}$+1-$\frac{5}{3}$π | C. | 2$\sqrt{3}$+2-$\frac{1}{2}$π | D. | $\sqrt{3}$+1-$\frac{1}{2}$π |
3. 如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D落在EG上,则旋转的度数为( )
如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D落在EG上,则旋转的度数为( )
 如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D落在EG上,则旋转的度数为( )
如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D落在EG上,则旋转的度数为( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
4.计算$\frac{2x+y}{x-y}$-$\frac{x+2y}{x-y}$的结果是( )
| A. | 1 | B. | $\frac{x+3y}{x-y}$ | C. | x-y | D. | x+3y |