题目内容
8. 如图,菱形ABCD的周长为8cm,高AE的长为$\sqrt{3}$cm,则对角线BD的长为( )
如图,菱形ABCD的周长为8cm,高AE的长为$\sqrt{3}$cm,则对角线BD的长为( )| A. | 2cm | B. | 3cm | C. | $\sqrt{3}$cm | D. | 2$\sqrt{3}$cm |
分析 首先设AC,BD相较于点O,由菱形ABCD的周长为8cm,可求得AB=BC=2cm,又由高AE长为$\sqrt{3}$cm,利用勾股定理即可求得BE的长,继而可得AE是BC的垂直平分线,则可求得AC的长,继而求得BD的长,则可求得答案.
解答  解:如图,设AC,BD相较于点O,
解:如图,设AC,BD相较于点O,
∵菱形ABCD的周长为8cm,
∴AB=BC=2cm,
∵高AE长为$\sqrt{3}$cm,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=1(cm),
∴CE=BE=1cm,
∴AC=AB=2cm,
∴△ACB是等边三角形,
∴OA=1cm,AC⊥BD,
∴OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=$\sqrt{3}$(cm),
∴BD=2OB=2$\sqrt{3}$cm,
故选:D.
点评 此题考查了菱形的性质以及勾股定理.注意菱形的四条边都相等,对角线互相平分且垂直.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是( )
| A. | 7,24,25 | B. | $\frac{7}{2}$,$\frac{9}{2}$,$\frac{11}{2}$ | C. | 3,4,5 | D. | 4,$\frac{15}{2}$,$\frac{17}{2}$ |
20.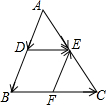 如图,已知在△ABC中,点D、E、F分别是AB、AC、BC的中点.下列结论不正确的是( )
如图,已知在△ABC中,点D、E、F分别是AB、AC、BC的中点.下列结论不正确的是( )
 如图,已知在△ABC中,点D、E、F分别是AB、AC、BC的中点.下列结论不正确的是( )
如图,已知在△ABC中,点D、E、F分别是AB、AC、BC的中点.下列结论不正确的是( )| A. | $\overrightarrow{DE}$∥$\overrightarrow{BC}$ | B. | $\overrightarrow{AD}-\overrightarrow{AE}=\overrightarrow{DE}$ | C. | $\overrightarrow{DB}$=$-\overrightarrow{FE}$ | D. | $\overrightarrow{DB}+\overrightarrow{DE}+\overrightarrow{FE}=\overrightarrow{DE}$ |
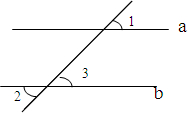 填空:如图,已知∠1=∠2,求证:a∥b
填空:如图,已知∠1=∠2,求证:a∥b 已知函数y=kx+b的图象与x轴、y轴分别交于点A(12,0)、点B,与函数y=x的图象交于点E,点E的横坐标为3,求:
已知函数y=kx+b的图象与x轴、y轴分别交于点A(12,0)、点B,与函数y=x的图象交于点E,点E的横坐标为3,求: 如图,∠C=59°,∠E=50°,AB∥CD,则∠EAB=109°.
如图,∠C=59°,∠E=50°,AB∥CD,则∠EAB=109°.