题目内容
13.如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是( )| A. | 7,24,25 | B. | $\frac{7}{2}$,$\frac{9}{2}$,$\frac{11}{2}$ | C. | 3,4,5 | D. | 4,$\frac{15}{2}$,$\frac{17}{2}$ |
分析 依次计算每个选项中两个较小数的平方的和是否等于较大数的平方,等于则能组成直角三角形,不等于则不能组成直角三角形.
解答 解:A、因为72+242=252,所以该组数能组成直角三角形;
B、因为$(\frac{7}{2})^{2}+(\frac{9}{2})^{2}$≠$(\frac{11}{2})^{2}$,所以该组数不能组成直角三角形;
C、因为32+42=52,所以该组数能组成直角三角形;
D、因为42+$(\frac{15}{2})^{2}$=$(\frac{17}{2})^{2}$,所以该组数能组成直角三角形;
故选B.
点评 本题考查了勾股定理的逆定理,运用勾股定理的逆定理解决问题的实质就是判断一个角是不是直角;注意:要判断一个角是不是直角,先要构造出三角形,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8. 如图,菱形ABCD的周长为8cm,高AE的长为$\sqrt{3}$cm,则对角线BD的长为( )
如图,菱形ABCD的周长为8cm,高AE的长为$\sqrt{3}$cm,则对角线BD的长为( )
 如图,菱形ABCD的周长为8cm,高AE的长为$\sqrt{3}$cm,则对角线BD的长为( )
如图,菱形ABCD的周长为8cm,高AE的长为$\sqrt{3}$cm,则对角线BD的长为( )| A. | 2cm | B. | 3cm | C. | $\sqrt{3}$cm | D. | 2$\sqrt{3}$cm |
18.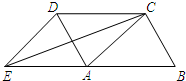 已知:如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为矩形的是( )
已知:如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为矩形的是( )
 已知:如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为矩形的是( )
已知:如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为矩形的是( )| A. | AC=CD | B. | AB=AD | C. | AD=AE | D. | BC=CE. |
5. 如图,在?ABCD 中,已知 AE、CF 分别是∠DAB、∠BCD 的角平分线,则下列说法正确的是( )
如图,在?ABCD 中,已知 AE、CF 分别是∠DAB、∠BCD 的角平分线,则下列说法正确的是( )
 如图,在?ABCD 中,已知 AE、CF 分别是∠DAB、∠BCD 的角平分线,则下列说法正确的是( )
如图,在?ABCD 中,已知 AE、CF 分别是∠DAB、∠BCD 的角平分线,则下列说法正确的是( )| A. | 四边形AFCE是平行四边形 | B. | 四边形AFCE是菱形 | ||
| C. | 四边形ABCF是等腰梯形 | D. | 四边形AECD是等腰梯形 |
2.下列命题不正确的是( )
| A. | 两直线平行,同位角相等 | |
| B. | 两点之间直线最短 | |
| C. | 对顶角相等 | |
| D. | 从直线外一点到直线上的所有线段中,垂线段最短 |
 用尺规作一个角等于已知角的和,要求不写作法,但要保留作图痕迹;已知:∠1、∠2.求作:∠AOB,使∠AOB=∠1+∠2.
用尺规作一个角等于已知角的和,要求不写作法,但要保留作图痕迹;已知:∠1、∠2.求作:∠AOB,使∠AOB=∠1+∠2. 如图直线AB⊥CD,垂足为O,直线EF过点O,且∠1=30°,求∠2、∠3的度数.
如图直线AB⊥CD,垂足为O,直线EF过点O,且∠1=30°,求∠2、∠3的度数.