题目内容
16．
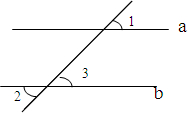填空：如图，已知∠1=∠2，求证：a∥b证明：∵∠1=∠2（已知）
∠2=∠3（对顶角相等）
∴∠1=∠3（等量代换）
∴a∥b（同位角相等，两直线平行）
分析 根据对顶角相等，以及已知角相等，等量代换得到一对同位角相等，利用同位角相等两直线平行即可得证．
解答 证明：∵∠1=∠2（已知）
∠2=∠3（对顶角相等）
∴∠1=∠3（等量代换）
∴a∥b（同位角相等，两直线平行），
故答案为：对顶角相等；∠3；等量代换；同位角相等，两直线平行
点评 此题考查了平行线的判定，熟练掌握平行线的判定方法是解本题的关键．
练习册系列答案
相关题目
如图，活动衣帽架由三个相同菱形组成，利用四边形的不稳定性，调整菱形的内角A，使衣帽架拉伸或收缩，若菱形的边长等于10cm，∠A=120°，则AB=10cm．AD=30cm．
7．
如图，将正方形ABCD的一角折叠，折痕为AE，∠B′AD比∠BAE大39°．设∠BAE和∠B′AD的度数分别为x，y，那么x，y所适合的一个方程组是（ ）
如图，将正方形ABCD的一角折叠，折痕为AE，∠B′AD比∠BAE大39°．设∠BAE和∠B′AD的度数分别为x，y，那么x，y所适合的一个方程组是（ ）| A． | $\left\{\begin{array}{l}{y-x=39}\\{y+x=90}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{y-x=39}\\{y+2x=90}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{y-x=39}\\{y=2x}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x-y=39}\\{y+2x=90}\end{array}\right.$ |
如图直线AB⊥CD，垂足为O，直线EF过点O，且∠1=30°，求∠2、∠3的度数．
8．
如图，菱形ABCD的周长为8cm，高AE的长为$\sqrt{3}$cm，则对角线BD的长为（ ）
如图，菱形ABCD的周长为8cm，高AE的长为$\sqrt{3}$cm，则对角线BD的长为（ ）| A． | 2cm | B． | 3cm | C． | $\sqrt{3}$cm | D． | 2$\sqrt{3}$cm |
5．
如图，在?ABCD 中，已知 AE、CF 分别是∠DAB、∠BCD 的角平分线，则下列说法正确的是（ ）
如图，在?ABCD 中，已知 AE、CF 分别是∠DAB、∠BCD 的角平分线，则下列说法正确的是（ ）| A． | 四边形AFCE是平行四边形 | B． | 四边形AFCE是菱形 | ||
| C． | 四边形ABCF是等腰梯形 | D． | 四边形AECD是等腰梯形 |