题目内容
1．[4（x+y）（x-y）-（x-y）2]÷y，其中x=$\frac{1}{2}$，y=3．分析 原式中括号中利用平方差公式及完全平方公式化简，去括号合并后利用多项式除以单项式法则计算即可得到最简结果，把x与y的值代入计算即可求出值．
解答 解：原式=（4x2-4y2-x2+2xy-y2）÷y=（3x2+2xy-5y2）÷y=$\frac{3{x}^{2}}{y}$+2x-5y，
当x=$\frac{1}{2}$，y=3时，原式=$\frac{1}{4}$+1-15=-13$\frac{3}{4}$．
点评 此题考查了整式的混合运算-化简求值，熟练掌握平方差公式及完全平方公式是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
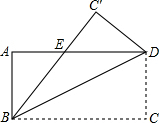如图，将长方形ABCD沿对角线BD折叠，使C恰好落在C'位置，∠DBC=25°，则∠ABC'=40°．
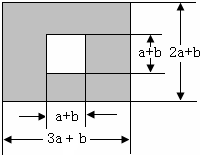如图，某校有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，学校计划将阴影部分进行绿化，中间将修建一座雕像．
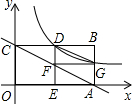如图，已知矩形OABC中，点A（2，0）、C（0，1）．点D是边BC的中点，过点D作DE⊥OA于点E，双曲线y=$\frac{k}{x}$过点D交AB于点G，直线AC交DE于点F，连接DG、FG．